このページへのアクセスは
このページへのアクセスは 人目です。(Since 2000/04/15)
経済数学入門
財政学は、応用経済学のなかでは比較的数学を使用しない科目と言えます。そのため、数学嫌いの人が履修することも多いのですが、やはり最低限の経済数学を身につけて欲しいものです。少なくとも私の科目で単位を修得するには以下で解説する最低限の数学が必要となります。
1.一次関数
経済学では、やたらと難しそうな関数が沢山でてきます。効用関数、生産関数、など・・・・
経済学で関数を使用するのは、所得、消費、投資といった経済変数間には、何らかの関係が存在すると考えられるからです。マクロ経済学の最初にでてくる関数に、消費関数というのがありますよね。これは、所得と消費の間の関係を示したものです。直感的に考えてもお金持ちほど、消費額は大きくなりそうですよね。まあ中には、貧乏にもかかわらず浪費癖がある人もいますが・・・。でも、経済学ではそんな特殊な人を想定するのではなく、平均的な個人の行動を想定します。その方がずっと自然ですよね。
消費関数に話を戻すと、いわゆるケインズタイプの消費関数は、数学的には1次関数で表現されます。
すなわち、消費をC、所得をYとおくと
C=a+bY
という式になります。ここで数学的にはaは切片、bは傾きとなります。さて、ここで問題です。いま、a=10、b=0.6と数値例が与えられたとき、縦軸に消費、横軸に所得をとったときにこの消費関数のグラフを書いてみてください。
2.二次関数
一次関数のグラフは、解答をするまでもないですよね・・・。それではほんの少しだけ難しくしましょう。経済学では、2次関数も時々使います。二次関数の式は、
y=x2
ですよね。さて、またまた問題です。2次関数のグラフを書いてみましょう。これも答え合わせ不要ですよね・・・
ここまでは、楽勝ですね。でもここから難しくなります。分数関数って知ってますか?
U=XY
という形の関数が分数関数です。どこが分数なんだというあなた、両辺をXで割ってみましょう。
Y=U/X
になり、分数になるでしょう。それでは、この関数のUの値が24のときのグラフを書けますか?数学が得意だった方は覚えているでしょう。これは直角双曲線になります。でも経済学では、マイナスの領域は扱わないのでプラスの領域に、原点に対して凸の曲線が描かれることになります。要するに無差別曲線や等産出量曲線は、このタイプの関数もとで描かれることになります(ミクロ経済学やマクロ経済学に出てくるコブダグラス型関数もこの親戚ですね・・・)。
さて、グラフが書けなかった人のために、この関数のグラフの書き方を伝授しましょう。y=f(x)の形の関数であれば、基本的にはxの任意の値を与えれば、yの値が計算できますから、面倒でもすこしずつxの値を変化させてyの値を計算してその軌跡をとればグラフは簡単に書けます。
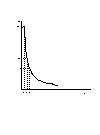 要するにx=1のときは、yの値はy=24/1=24ですよね。
要するにx=1のときは、yの値はy=24/1=24ですよね。
x=2のときは、yの値はy=24/2=12になります。
x=3のときは、yの値は8
x=4のとき、yの値は6
というように、全部計算していけば、方眼紙でも買ってくれば縦軸をy、横軸をxとしたときのグラフを書けるでしょう。
4.微分
経済学を理解するには、微分は欠かせません。高校で、微分がでてきたときには、私も何の役に立つのだろうと思ったものですが・・・
(1)微係数
微分が便利なのは、グラフを使わなくても関数の形が推測できるところにあります。与えられた関数を任意のxで微分するとその関数の接線の傾きが得られるからです。接線って何か覚えてますか?中学のときに数学の先生が黒板に適当な曲線のグラフをかいて、そのグラフに接する線を定規で引いてませんでしたか?
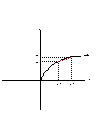
それでは実際に適当な曲線の接線を引いてみましょうか。下のグラフをみてください。
←クリックすると大きな絵が見られます。
この図では、ある関数y=f(x)のグラフが描かれています。いまx1に対応する値はy1ですね。そこでこのxの値を少し増やすことにしましょう。でもあまり増加分が小さいとみえないので、x2まで増やしてみました。当然、yの値はy2まで増加します。
そこで、いまxの増加分をΔx、yの増加分をΔyとしましょう。このΔという記号はさんかくと呼ぶのでなく、デルタといいます。数学ではこれは増分を表す記号です。
このyとxの増加分のわり算をしてみましょうか。つまり△y/△xを求めると傾きが得られます。グラフでは赤い点線の傾きが計算できることになります。でもこの赤い点線ともとの関数y=f(x)のグラフとの間にはすきまがあります。しかし、xの増加分をすこしずつ小さくしていくとこのすきまも小さくなっていきます。グラフを書くとわかりやすいのでしょうが面倒なので自分で書いてね・・・
xの変化をゼロに近づけていくと最終的には、△y/△xで得られる赤い点線の傾きは、任意の点での接線と一致するわけです。
微分をすると接線の傾きがわかるのです。でも接線の傾きがわかって何の役に立つのでしょうか?それは経済学では、関数の最大値や最小値を求める問題がでてくるからです。たとえば、企業の目的は、お金儲けですよね。経済学的に言うと利潤最大化行動をとっていると考えられます。いま、企業が生産量を増やしたときの利潤が下のグラフのようになるとしましょう。
利潤のグラフ
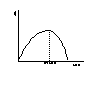
最適な生産量は、あきらかに山の一番高いところから垂直に点線をひいてえられるところですよね。このような最大値は、微分を利用すれば簡単に計算できます。つまり、山の一番高いところで接線を引いてやればいいのです。もしこのグラフで山の頂点で接線を引くとその接線は水平になりますよね。水平線の傾きはゼロです。だから、利潤最大化のためには接線の傾きがゼロでなければならないことがわかります。ただし、接線の傾きがゼロになるケースは必ずしも最大値とは限りません。いまU字型の曲線を描いたとしましょう。この曲線に対して傾きがゼロになるような接線を引いたとすると、最小値が得られます。つまり、一度微分しただけでは、最大値か最小値かどちらかまではわかりません(グラフを見るとすぐわかるでしょうが・・・・)。そこで、一度微分して求めた条件は、一階の必要条件といいます。(1回でなく1階です、なぜだが知りませんが・・・)
(2)微分公式
さて、微分を使うと便利なことが何となくわかっていただけたでしょうか?この微分を使うためには、微分公式を暗記しなければなりません。そんなに難しくないので覚えてくださいね。
y=axn
dy/dx=n・a・xn−1
これが公式です。dy/dxはyをxで微分することを意味しています。
それでは、問題です。
y=x2
をxで微分してね。簡単ですよね。答えは2xです。では
y=x
をxで微分してみましょうか。これは少し難しいですね。公式のaとnに当たる数字が明記されてませんよね。これは書いてませんが、aとnはそれぞれ1で省略されていると解釈してください。したがって、
dy/dx=1×1×X1-1=X0=1
となります。ある変数のゼロ乗は1ですから・・・(なぜかは忘れましたが・・・)
では
y=x2+4
を微分するとどうなるでしょうか。答えは
dy/dx=2x
となります。つまりy=x2 をxで微分した答えも、 y=x2+4 をxで微分した答えも全く同じになります。なぜでしょうか?下の図をみてください。
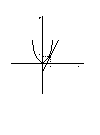
まずy=x2 という関数を微分すると接線の傾きが2xとなるので、かりにx=2のところで接線をとると傾き4となる状況が描かれています。
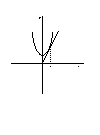
次にy=x2+4のグラフをみてみましょう。このグラフはy=x2のグラフを平行に上に移動すればかけますよね。だから、かりにX=2のところで接線を描くとやはり傾きは4になるわけです。つまり微分をおこなうときに、+4という定数の部分は何ら影響をあたえないことになるのです。この定数は微分において無視できるというのは、よく考えてみるとあたりまえでしょう。微分というのはxが微少な変化したときにyがどれだけ変化するかをみるものですよね。だから定数の部分は、いくらであってもxが変化してもyの変化に何ら影響を与えないので、無視できるのです。
(3)偏微分
微分の親戚に偏微分というのがあります。偏微分の偏は、変人の変でなく、偏るという字を使います。つまり偏った微分ですね。これは、他の変数を一定として微分することを意味します。微分において定数は無視するのでしたね。
とりあえず、例題を解いてみましょう。やってみると意外と簡単ですから・・・
z=2x2y2+3y
という関数をxとyについて偏微分してみましょう。まずzをxで偏微分すると
∂z/∂x=2×2y2×X2-1=4xy2
↑ ↑ ↑
n a xn-1
となります。∂は偏微分の記号です。xで偏微分するときyは定数として考えるわけなので3yの部分は無視していいわけです。y2
の部分も定数だと考えます。
次にzをyで偏微分すると、今度はxを定数と考えるので
∂z/∂y=2×2x2×y2-1+1×3×y1-1=4x2y+3
となります。今度は3yの部分をyで微分しなければならないところに注意しましょう。
5.制約条件付き最大・最小:一階の必要条件
さて、経済学を学ぶうえで極めて便利な解法を伝授しましょう。経済学では、制約条件付き最大化、最小問題がよく出てきます。たとえば、消費者の理論では、消費者は予算制約のもとで効用を最大化するのでしたね。企業は所与の生産量を制約として費用を最小にするように生産要素を選択します。詳しくは、ミクロ経済学入門を乞うご期待・・・。この制約条件付き最大化問題に使われるのがラグランジェ乗数法です。機動戦士ガンダムのスペースコロニーは地球と月の間の重力つりあうポイント、ラグランジュポイントにおいてたのを覚えていますか?ラグランジュというのは数学者の名前で、ラグランジュのおかげでいまロケットが打ち上げられているのです・・・・ このラグランジュ乗数法は、偏微分がわかれば誰でも使えます。ただし、これでなぜ制約条件付き最大、最小問題が解けるのかは、むずかしすぎて私にもさっぱりわかりません。でも数学者以外は証明がわからなくてもかまいませんからご安心を。
まず以下のような制約条件付き、最大化問題が与えられているとしましょう。
Max f=f(x,y)
Sub.to g(x,y)=0
この表記方法は、g(x,y)=0を制約として(subject
to)、 f=f(x,y)という目的関数を最大化(Max)しなさいということを意味しています。この問題をとくには、目的関数と制約条件、そして制約条件にあらたな変数として、λで示されるラグランジュ乗数を加えて、ラグランジュ関数Lをまず定義します。つまり
L=f(x,y)+λg(x,y)
という式になります。このラグランジュ関数をx、y、λで偏微分してえられる方程式をゼロとおき、その連立方程式をx,yについて解けば、制約条件をみたしながら、目的関数を最大ないし、最小にするようなx、yの値が求まります。つまり、ラグランジュ関数をx、y、λで偏微分し、ゼロとおくと
Lx =fx+λgx =0
Ly =fy+λgy =0
Lλ =g(x,y) =0
となるでしょう。ここで下付の添え字は、偏微分を意味しています。たとえばLxは∂L/∂xを意味します。下付で書いた方が見やすいので、経済学の論文のほとんどで偏微分は下付添え字で表記されています。この3つの式からλを消去し、x、yについて解くだけです。
少し難しそうですが、実際にやってみると微分さえできれば以外と簡単です。では以下の例題をといてみましょう。
例題
max u=xy
sub.to 4=x+y
Lx=y−λ=0 (1)
Ly=x−λ=0 (2)
Lλ=x+y−4=0 (3)
(1)(2)より x=y
(3)に代入 y−y=4
y=2、x=2
となります。
ミクロ経済学入門
財政学の教科書には、無差別曲線を使った分析が出てきます。しかし、無差別曲線そのものの説明は全くといってなされていないのが現状です。つまり財政学を学ぶ際には、入門レベルのミクロ経済学の学習を終えていることを前提としているわけです。しかし、財政学の履修者は、必ずしもミクロ経済学を修得しているとは限らないのが現状です。そこで、ここでは、財政学を学ぶうえで最低限知っておいて欲しいミクロ経済学のポイントを解説することにしましょう。
さて、ミクロ経済学とはどういう学問でしょうか。実は簡単なミクロ経済学はすでに高校の政治経済でも学んだはずなのです。市場での価格と需要は、需要曲線と供給曲線の交点で得られるというのを勉強したでしょう・・・一般に、需要曲線は右下がりで、供給曲線は右上がりになります。この需要曲線と供給曲線はどのようにして導出できるのでしょうか。ミクロ経済学では、需要曲線は、消費者(家計)の最適化行動、供給曲線は生産者(企業)の最適化行動から導かれると考えます。
1.消費者行動の理論
さて、消費者はどのような最適化行動をとると考えられるのでしょうか。消費者行動の理論では、消費者は、予算制約のもとで効用(満足度)を最大にするように行動すると考えます。
(1)予算制約
まず、予算制約から説明しましょう。果物屋さんにりんごとみかんを買いに行くことになったとしましょう。さいふの中には1000円札が入っています。リンゴは1個50円で、みかんは1個100円で売っていたとしましょう(ずいぶん高いみかんですが、千両みかんという落語もあることですし、許してね・・・)。
いま持っているお金を全部りんごにつぎこむといくつ買えますか。1000/50=20個買えますね。一方、全部みかんを買うといくつ買えますか1000/100で10個ですね。でも全部みかん、ないし、りんごというのでは飽きてしまうのでりんごとみかんをまぜて買うことにしましょうか。しかも、あなたは江戸っ子で持っているお金はきれいに全部使わないと気が済まない質だとしましょう。持っているお金でりんごとみかんを何個買えるかをします式をミクロ経済学では消費者の予算制約式と呼んでいます。この場合だと、みかんの数量をx、りんごの数量をyとおくと
100x+50y=1000円
となります。たとえばりんごを2個買うとすると
100×x+50×2=1000
ですから、みかん、xの数量が9個のときにちょうど1000円になるでしょう・・・
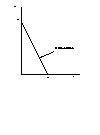 ではこの消費者の予算制約式をグラフにしてみましょう。縦軸にりんごの数量y、横軸にみかんの数量xをとると、まず全部りんごを買うと20個買えますよね。このときみかんは買えませんのでy軸上にりんご20個とみかん0個の組み合わせを示す点をとることができます。次に全部みかんを買うとしましょうか。このときみかんは10個買えますがりんごは買えません。するとx軸上にりんご0個とみかん10個の組み合わせを示す点をとることができます。この2つの点を結ぶと消費者の予算制約線が得られます。消費者はこの予算制約線の上の組み合わせではちょうど持っているお金を全部使ってりんごとみかんを買うことになります。かりにこの予算制約線の内側の領域を選択した場合には、予算が余ることになります。この予算制約線上とその内側の領域は、消費可能領域と呼ばれます。
ではこの消費者の予算制約式をグラフにしてみましょう。縦軸にりんごの数量y、横軸にみかんの数量xをとると、まず全部りんごを買うと20個買えますよね。このときみかんは買えませんのでy軸上にりんご20個とみかん0個の組み合わせを示す点をとることができます。次に全部みかんを買うとしましょうか。このときみかんは10個買えますがりんごは買えません。するとx軸上にりんご0個とみかん10個の組み合わせを示す点をとることができます。この2つの点を結ぶと消費者の予算制約線が得られます。消費者はこの予算制約線の上の組み合わせではちょうど持っているお金を全部使ってりんごとみかんを買うことになります。かりにこの予算制約線の内側の領域を選択した場合には、予算が余ることになります。この予算制約線上とその内側の領域は、消費可能領域と呼ばれます。
この消費者の予算制約式を一般的に定義するために、数値例を記号におきかえましょうか。
りんごの価格をp1、みかんの価格をp2、予算をMとすると
p1x+p2y=M (1) 消費者の予算制約式
となります。
(2)効用と無差別曲線
さて、消費者の予算制約線上の組み合わせでりんごとみかんを購入すれば、と持っているお金がちょうど全部なくなることがわかりました。でも、この組み合わせは(かりにりんごとみかんを1個づつでなく、小分けにして買うならば)無数にありますよね。スイカじゃあるまいしという話もありますが・・・この無数の組み合わせの中から消費者はどのような選択をすればよいのでしょうか?ミクロ経済学では、消費者は、効用(財・サービスから得られる満足度)を最大にするように選択するものと考えます。では、この満足度はどのようにすればわかるのでしょうか?一番簡単なのは次のようなアンケート調査に記入することです。いまあなたにとって満足だといえるりんごとみかんの組み合わせをひとつだけ教えてくださいと言われたとしましょう。そこであなたは、自分にとって満足だと言える組み合わせを
満足だ=りんご24個とみかん1個
と答えたとしましょう。ところが果物屋さんには、りんごは24個しかなかったとしましょう。そこで、果物屋さんに「お客さん、すみませんあいにくりんごはいま12個しかありません、かわりにみかんを余分に買うということにしてもらえませんか」と言われました。そこで、あなたはりんごをあきらめてかわりにみかんを余分に買うことにしました。あなたはりんごをあきらめるかわりにみかんを買うことにしました。よく見るとりんごは安いかわりにかなり傷んでいます。それに比べてみかんはいかにもおいそうです。これならりんごを12個あきらめるかわりに、みかんをあと1個買えば十分だとあなたは考えたとしましょう。すると、このりんご12個とみかん2個という新しい組み合わせは、最初の組み合わせと同じ満足度を達成できることになります。つまり
満足だ=りんご12個とみかん2個
ですよね。
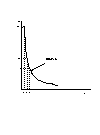 この2つの組み合わせのパターンをグラフにしてみましょう。縦軸にはりんごの数量、横軸にはみかんの数量をとります。すると24個と1個のところに点がひとつそして、12個と2個のところにも点がとれます。どうせならもっとたくさんの組み合わせも書き入れましょう。そのときの約束事は、あなたにとって満足だと言える別の組み合わせを書き入れることだけです。最終的にあなたは
この2つの組み合わせのパターンをグラフにしてみましょう。縦軸にはりんごの数量、横軸にはみかんの数量をとります。すると24個と1個のところに点がひとつそして、12個と2個のところにも点がとれます。どうせならもっとたくさんの組み合わせも書き入れましょう。そのときの約束事は、あなたにとって満足だと言える別の組み合わせを書き入れることだけです。最終的にあなたは
りんご 24個 みかん 1個
12 2
8 3
6 4
4 6
のすべてが満足だという組み合わせだということをアンケート用紙に書き入れました。この組み合わせを線でなめらかな線で結んでみましょう(グラフでは少しごつごつしてますが、ご容赦のほどを・・・)。どこかでみたようなグラフだと思いませんか。そうです、分数関数のグラフと同じでしょう。 この曲線は、同じ満足度、効用水準を結んだものですから、曲線上ではどの点を選んでも後悔しないはずです。どこでも同じという意味でこの曲線は消費者の無差別曲線と呼ばれます。
さて、いまこのようにして描いた無差別曲線は満足だという効用水準を達成するものと考えられます。そこで、いまあなたは、最初の24個1個という買い物をしようしたとしましょう。すると、果物屋さんが「毎度どうも、今日はおまけをしてあげましょう。みかんを1個おまけにどうぞ」と言いました。どうですか、うれしいですよね。当然満足度はりんご24個とみかん1個のときより、りんご24個とみかん1個のときの方が上昇します。この満足度を非常に満足だという満足度だとしましょう。そこでこの非常に満足だという組み合わせを基準としてさきほどと同じように同じ満足度、効用水準を達成するような無差別曲線を書いてみましょう。すると、このあらたなより高い満足度を示す無差別曲線は、最初の無差別曲線よりも右上方に描かれることになります。このようにすれば、無差別曲線は、等高線のように無数に描かれれていくことになります。
さて、この無差別曲線を式で示してみましょう。無差別曲線は、ある特定の効用水準(記号Uで示しましょう。これは効用を英語ではutilityと書くところからきています。)Uを達成するような、みかんの数量x、りんごの数量yの組み合わせを示すことになります。これを一般的な関数で表記すると
効用関数 U=U(x,y)
となります。さきほどはU=xyという特定の関数を仮定していたことになります。 実証分析では、実はもう少し複雑な関数形をよく使います。たとえばコブダグラス型効用関数とかCES型効用関数などですが、学部生は知らなくてもかまいません。大学院にいくひとはミクロ経済学のテキストで調べてくださいね。この効用関数については、いろいろと大事な性質があるのですが、最低限覚えて欲しいのが、限界代替率逓減の法則です。限界代替率(Maginal Rate of Substitution:MRS)とは、無差別曲線の傾きのことです。この傾きは、グラフをみるとわかるように、だんだんと傾きがゆるくなっていきます。これは、「ある財が他財に比べて、相対的に少なくなれば、希少性が増す。
」からだと説明できます。つまり最初のうちは、りんごとみかんの交換のときに気前よくりんごを減らしていました。でも、気がつくとりんごの方がみかんより少なくなってきました。すると最初は傷んでいるからいいやとおもっていたのですが、だんだんと惜しくなってきました。最後の1個になると絶対に手放したくなりました。というお話が成立するとミクロ経済学では想定します。でも中には数が少なくなっても惜しくないといいはる人もいるでしょう。でも、経済学ではあくまでも平均的な消費者を想定します。その方がみのりある議論ができますし・・・
(3)消費者の効用最大化
さて、(1)消費者の予算制約と(2)消費者の無差別曲線を組み合わせると、消費者の効用最大化が得られます。まず、図解による説明をしてみましょう。
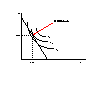 左の図には、消費者の予算制約線と無差別曲線が重ね合わせて描かれています。無差別曲線は、無数にひくことができるのですが、面倒なので3本だけ書いてあります。この3本の無差別曲線の中で最も消費者の効用水準が高くなるのはどこかわかりますか。無差別曲線は、右上方へいくほど効用水準が高くなるので、正解はU2です。でもこの無差別曲線は消費可能領域のはるか上にありますよね。つまりこの組み合わせを選択しようとするとお金が足りなくなります。消費者にとって予算の範囲内におさまるのは、U0とU1の無差別曲線です。この2つのうちでは、U1の無差別曲線の方が効用は高くなります。つまり、消費者の効用最大化は、予算制約線と無差別曲線が接するところで得られることになります。
左の図には、消費者の予算制約線と無差別曲線が重ね合わせて描かれています。無差別曲線は、無数にひくことができるのですが、面倒なので3本だけ書いてあります。この3本の無差別曲線の中で最も消費者の効用水準が高くなるのはどこかわかりますか。無差別曲線は、右上方へいくほど効用水準が高くなるので、正解はU2です。でもこの無差別曲線は消費可能領域のはるか上にありますよね。つまりこの組み合わせを選択しようとするとお金が足りなくなります。消費者にとって予算の範囲内におさまるのは、U0とU1の無差別曲線です。この2つのうちでは、U1の無差別曲線の方が効用は高くなります。つまり、消費者の効用最大化は、予算制約線と無差別曲線が接するところで得られることになります。
この条件は、数学的にはどのように表記されるのでしょうか。その問題は、ラグランジュ乗数法を利用することで、簡単に解くことができます。すなわちこの問題は
Max U=U(x,y) 効用関数
Sub.to. M=p1x+p2y 消費者の予算制約
という、制約条件付き最大化問題と解釈できるので、ラグランジュ関数は
L=U(x,y)+λ[M-p1x-p2y]
と定義されます。ただしλはラグランジュ乗数です。これを解くには、ラグランジュ関数Lを選択変数であるx、yとラグランジュ乗数λで偏微分してゼロとおけばよかったのですね。すなわち
Lx=Ux−λp1=0 (1)
Ly=Uy−λp2=0 (2)
Lλ=M-p1x-p2y=0 (3)
となります。ここでUx=∂U/xつまりx財の限界効用、Uy=∂U/∂yつまりy財の限界効用を意味しています。まず、(1)(2)式を変形しましょう。(1)式は
Ux/p1=λ (1)'
そして(2)式は
Uy/p2=λ (2)’
と書き換えることができます。したがって(1)'(2)'よりλを消去すれば
Ux/p1=Uy/p2 (4)
という式が導出できます。この式は。効用最大化のための1階の必要条件であり、限界効用均等の法則と呼ばれています。
この(4)式は、さらに左辺の分母と右辺の分子を交換すると
Ux/Uy=p1/p2
という式に書き換えることもできます。つまり、消費者の予算制約のもとで効用を最大化するためには、
限界効用の比が価格比に等しくなければなりません。この左辺は無差別曲線の傾き、限界代替率を示しています。
したがってこれは
限界代替率(MRS)=価格比
という条件でもあります。要するに、グラフで説明したように無差別曲線の傾きと予算線の傾きが等しいところで効用最大化が
得られるということをこの式は示していることになります。
(4)需要曲線の導出
消費者の需要曲線は、この消費者の予算制約と無差別曲線を使うことで、導出できます。
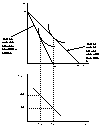 左の上の図には消費者の無差別曲線と予算線が描かれています。
左の上の図には消費者の無差別曲線と予算線が描かれています。
予算線と無差別曲線はそれぞれ2本あります。これはりんご50円、みかん
100円、予算が1000円という上で説明した効用最大化問題に加えて、みかんの値段が50円に値下げされた場合を付け加えたものです。もしみかんの値段が100円から50円に値下げされたならば、1000円の予算を全部みかんにつぎ込むと20個買えることになります。一方、りんごの値段はかわらないとすると、全部りんごにお金を使った場合に買うことのできるりんごの数は20個のままです。したがって、みかんの値段が50円になると、消費者の予算制約は
y軸上の切片を中心に回転することになり図のように傾きがゆるくなります。予算制約線が変化すると、無差別曲線との接点も当然図のように変化します。
この価格変化前と変化後における予算制約線と無差別曲線の接点を垂直おろすことで、みかんの数量の変化が横軸のうえではかることができます。
下の図の縦軸にはみかんの価格をとります。値下げ前の100円のときのみかんの数量は上の図からX1、値下げ後の50円のときのみかんの数量はx2になることがわかりました。つまり価格がさがるとみかんの需要が増加することになります。みかんの値段を小刻みに変化させていくと、同様にしてみかんの需要量の変化がわかります。この価格の変化に対応した需要量の変化を描いたものが消費者の需要曲線です。
2.生産者行動の理論
以上のように、需要曲線は、消費者の効用最大化行動から導出できます。一方、供給曲線は、生産者(企業)の最適化行動から導きだすことができます。さて、生産者は何のために生産活動をおこなっているのでしょうか。ミクロ経済学では、通常の企業は利潤を最大化するように行動すると考えます。要するにお金儲けですね・・・お金儲けするために必要なことは何でしょうか。それは、できるだけ費用をかけずに、適正な数量の生産をおこなうことです。あまりたくさん生産して売れ残ってたら困りますし。
(1)費用の構造
いま世間では、リストラの嵐が吹き荒れているようですが、これも生産者が利潤を最大化しようとしている証です。できるかぎり少ない人数で同じ売り上げを達成できれば、利潤が増大するわけですから・・・でも個別企業にとっては、リストラはプラスでしょうが、リストラによる失業者の増大は、消費者の需要を低下させ、結局売り上げがのびないことにつながり、経済全体ではマイナスになる可能性もあります。単なる人減らしでなく、人員の有効な再配置が、本来のリストラクチャーの意味だと思うのですが・・・
それはさておき、生産者にとっての費用について考えてみましょう。総費用は、
総費用=固定費用+可変費用
機械設備などの固定費用と人件費などの可変費用から構成されると考えられます。もう少し具体的な例を考えてみましょう。どこの大学んでも秋になると学園祭がありますよね。この学園祭にサークルでたこ焼きの屋台を出すとしましょうか。最近は学生さん相手の業者がいて、たこ焼きの屋台一式を貸し出してくれるそうです。この屋台一式を借りるのに必要な費用が固定費用です。これは、たこ焼きの生産量に関わらず一定額の費用がかかるからです。したがって、少なくとも固定費用分だけは回収しないと大損ですよね。次に、可変費用ですがこれには人件費や材料費が入ります。生産量を増やそうと思えば人手を増やして、たこやきを一度にたくさん焼いて、そのたくさん焼いたたこやきをみんなで手分けして知り合いに売りつけないといけませんよね。私も大学生のときにはクラスで出店したのですが、お互いに友人のお店の商品を買ってました・・・。結局あんまりもうかりませんでした。それに学園祭のときには人件費はみなさんなぜか無視していますが、その時間、アルバイトにいった方が余程儲かっていたかもしれませんね。
さて、この費用に関してはいくつかの覚えて欲しい重要な概念があります。これらの概念は後で使うことになりますので、しっかり暗記しましょう。
その1 平均費用=総費用/生産量
まず平均費用を覚えましょう。これは総費用を生産量を割ったもので、生産1単位当たりの費用になります。縦軸に平均費用、横軸に生産量をとって描くと、U字型になるケースがよくミクロ経済学のテキストにでてきます。このようなU字型の平均費用曲線は、固定費用が存在することで発生します。つまり、生産量が少ないときは、固定費用があるので平均費用は高くなります。たとえばたこ焼きの屋台一式を借りるのに10万円かかったとしましょうか。もし1個しかたこ焼きをつくらないとすると、その1個には材料費・人件費を無視すると
10万円かかったことになりますよね。もし2個つくれば5万円に低下します。10個なら1万円、100個なら1000円、千個なら100円というように生産量が多くなるにしたがって、固定費用の重みは低下していきます。それでは、生産量は多いほどよいのでしょうか。いまの計算は、人件費と材料費を無視してました。でも人件費・材料費は生産量が増えるにしたがって増加していきます。それにlくわえて
1万個、2万個と売るならそれだけ人を集めるために広告宣伝費も必要となってくるでしょう。屋台も一台では足りなくなるでしょうし、全国展開も考えないといけなくなるでしょう。すると平均費用は再び増加していく可能性があります。したがって、平均費用曲線はU字型が想定されるケースもでてくるわけです。
その2 限界費用=総費用の増加/生産量の増加
平気費用以上に、経済学を学ぶうえで絶対に理解して欲しい概念が限界費用(Marginal
Cost;MC)です。これは総費用の増加分を生産量の増加分で割ったもので、生産量を増加させたときに、追加的に費用がどの程度増えるかを表したものです。総費用の増加分を生産量増加分でわるので
これは
限界費用=△総費用/△生産量
とも書けます。この△マークは数学では増分を意味するのでしたよね。この増分が微少な変化のときには、限界費用は、総費用を微分してやれば良いことになります。それではここで例題です。
例題:企業の費用関数がTC=x2+30で示されるものとしよう。ただしTCはtotal
cost総費用、xは生産量です。
a.総費用関数のグラフを書いてみましょう。縦軸には、総費用、横軸には生産量をとります。答え合わせは不要でしょう・・・・
b.平均費用のグラフを書いてみましょう。縦軸には平均費用、横軸には生産量をとります。
これはヒントをば・・・
まず、平均費用(Average Cost)は
平均費用 AC=TC/x=X+30/X
と総費用をxで割るとでます。後はグラフにするだけです・・・
c.限界費用を求めなさい。
これは少し難しいので解答です・・・
限界費用 MC=△(TC)/△x=2X
限界費用は総費用をxで微分するだけです・・・
(2)企業の利潤最大化
さて、それではいよいよどうすればお金儲けができるのかを伝授しましょう。 実は、企業の行動は、市場の状況によって左右されます。たとえば、学園祭であなたのサークルだけがたこ焼きの屋台を出しているケースと、無数のたこ焼きの屋台が出ている場合を考えてみましょう。あなたのサークルだけ出店しているならば、自分で価格を設定できますよね。でも無数の競争相手がいるなら、自分の都合だけでは価格は決められません。これは、完全競争市場において、企業がプライステイカー(price taker)として行動するケースです。ミクロ経済学では、前者のあなたのサークルだけ出店しているケースは独占と呼んでいます。これについてはミクロのテキストで勉強してくださいね・・・
それでは、完全競争市場の場合、企業の利潤を最大化するような最適な生産量は如何なる水準に決まるのでしょうか?まず、利潤を定義しましょう。利潤は
利潤=総収入−総費用
です。ここで総収入、つまり売り上げは、生産量に市場価格Pをかけたものになります。
利潤=価格*生産量−総費用
さてこの式を数式で表記しましょう。利潤はπ、生産量はx、総費用はCとしましょう。すると
利潤 π=px−C
となります。利潤を最大化するために必要な条件を求めるには、微分を使うと便利です。利潤を最大化するには、この式をxで微分したものをゼロとおき、式をときます(微分のところで書いた利潤のグラフを思い出してね・・・)
すなわち
dπ/dx=p−dC/dx=0
p=dC/dx
となります。ここで右辺のdC/dxはどこかでみた式ですね。総費用を生産量で微分したもの、すなわち限界費用です。だから、企業は
価格=限界費用 企業の利潤最大化の必要条件
が成立するように、生産量を設定すれば利潤を最大化することができます。
(3)企業の費用最小化
企業は利潤を最大化するように生産量を決定します。さて、企業が財・サービスを生産するためには、そもそも何が必要なのでしょうか?必ず必要なものが人手ですよね。社員ゼロの会社は、ありえないですから。それと工場をつくるには莫大なお金がかかるので、資金も調達しないといけませんね。工場をたてるには土地もいりますね。この3つが生産に必要とされる主要な生産要素としての労働、資本、土地です。それに原材料も必要ですね。原材料は、経済学では中間財投入などと呼びます。単純化のために、企業がある商品を生産するためには、労働と資本という生産要素のみが必要とされているとしましょう。いま、ある商品の生産量をQ、労働投入量をL、資本投入量をKとすると、生産量は、労働と資本の投入量に依存すると考えられるので、数学的に表記すると
Q=Q(K,L) 生産関数
となります。これは、生産関数と呼ばれます。この生産関数には、通常、限界生産物逓減の法則が成立すると考えられます。(この限界生産物逓減の法則と似た名前の法則として、生産関数について規模に関して収穫一定、規模に関して収穫逓減、規模に関して収穫逓増という性質がありますが、混同しないように)。たとえばある一定の面積の農地で農産物を生産する場合、人手を増やすほど、収穫量(生産量)は増大すると考えられます。でも、その増加の割合は少しずつ減少していくと考えられます。土地面積が限られているので、はじめは種を植える人、農薬をまく人、刈り入れをする人、水をまく人といくらでも仕事があるのでしょうが、そのうち人手を増やしても仕事がなくなり、邪魔なだけになってしまいますよね。この限界生産物逓減の法則は、数学的には
ΔQ/ΔL=MPL>0
ΔMPL/ΔL<0
と表記できます。まず、ΔQ/ΔLは、労働の増加分で生産量の増加分を割ったものです。これは労働の限界生産物marginal product of labor と呼びます。経済学のテキストの多くが英語の頭文字からMPLと表記しています。この労働の限界生産物は正、つまり労働投入を増加すると生産量も増加すると考えられます。ただし、その生産の増加割合は減少するので、ΔMPL/ΔL(労働の増加分で限界生産物の増加分をわったもの)が負になると考えられるわけです。なお、労働だけでなく、資本についても同様の法則が成り立つと考えられるので、資本の限界生産物MPKについても
ΔMPK/ΔK<0
が成立すると考えられます。
この生産関数をグラフに描いたものが等(産出)量曲線です。見た目は消費者の無差別曲線と同じです。等量曲線は、ある所与の生産量を達成するような生産要素の組み合わせを示しています。縦軸、横軸にはKとLをとって、原点に対して凸の曲線を自分で描いてみてくださいね。そしてその曲線を等高線のように描いた場合、原点より遠くなるにしたがって、生産量の水準が高くなることを、たとえばQ=KLという生産関数を想定して確かめてみてくださいね。このグラフの書き方は、経済数学入門の分数関数のところにありますから。
この等量曲線のなかで、利潤を最大化するような生産量を示すものをQ0としましょうか。これは、価格=限界費用という条件をみたすことで計算できるわけですね。このような最適な生産量を達成するような、生産要素の組み合わせを示しているが等量曲線ですから、その組み合わせは無数に存在することになります。企業は無数に存在する生産要素の組み合わせのなかからどの組み合わせを選択すればよいのでしょうか?労働や資本といった生産要素を投入するには、コストがかかります。もし、人件費の方が資本費用よりも相対的に安いならば、企業は資本の投入量が少なく、労働の投入量が多くなるような組み合わせを選択するでしょうし、逆に人件費の方が資本費用よりも相対的に高いならば、企業は資本の投入量が多く、労働の投入量が少なくなるような組み合わせを選択するでしょう。つまり、企業は費用を最小化するように生産要素の選択をおこなうものと考えられます。労働の1単位あたりのコストをw、資本の1単位あたりの価格をrとすると生産要素にかかる費用Cは
C=wL+rK
となります。この式を書き直すと
K=C/r−(w/r)L 等費用式
となります。この式は、切片がC/rで、傾きが−(w/r)の1次関数ですね。消費者の予算制約式と似てますね。ここで練習問題です。縦軸にK、横軸にLをとり、w=100、r=100、C=1000のグラフとw=100、r=100、C=2000のグラフを描いてみてください。資本と、労働の価格が一定のとき、コストCが大きくなるにしたがって等費用線が平行に右上に移動していくことが確認できるはずです。企業の費用最小化は、利潤を最大化するような最適な生産量のもとでの等量曲線とこの等費用線を組み合わせることで解が得られます。消費者の効用最大化と同様に、費用最小化は等量曲線と等費用線の接点で達成されます。これも自分で図をかいて確認してみてくださいね。この問題は、数学的には生産関数を制約とし、費用関数を目的関数とすることで解くことができます。つまり
min C=wL+rK 費用関数
SUb.to Q0=Q(L,K) 生産関数
となります。ここで生産関数は一定の生産量Q0のときのものとします。つまり、生産量の異なる水準について無数に描ける等量曲線のなかで、Q0という特定の水準の等量曲線だけを制約とするわけです。この問題にラグランジュ乗数法を適用すると
LL=w-λMPL=0
LK=r-λMPk=0
となるので、λを消去すると最終的に
MPL/MPk=w/r
という費用最小化の必要条件が導出されます。この式の左辺は等量曲線の傾き、右辺は要素価格比を示しています。この条件を満たす労働と資本を選択すれば、費用を最小化するという意味での最適な生産要素の組み合わせとなります。
(4)独占
ここまでの説明は、完全競争市場を想定してきました。しかし、ある財・サービスを提供しているのが1社のみという独占の場合は、話が違ってきます。完全競争市場の場合には各企業は市場できまった価格のもとで行動しています。しかし、分で価格を決定することができます。ただし、あまり高い値段をつけると需要が減少するので高ければよいというわけではありません。つまり、独占企業は、市場の需要曲線そのものに直面していることになります。いま、独占企業が直面している需要曲線が
P=100−Q
と描かれているとしましょう。ここでpは独占企業の生産物価格、Qは数量です。企業が製品の販売から得られる収入は、
総収入=価格×数量
ですね。たとえば1個100円のりんごを10個販売したら1000円の売り上げ(総収入)が得られます。完全競争市場の場合には、この価格は市場で決まるので販売量が増加しても変わらないのですが、独占企業の場合には、販売量が増えるにしたがって価格が減少していきます。数年前に「たまごっち」がはやりましたよね。発売当初はバンダイ1社で独占状態にあり、プレミアムがついてましたが、増産が進むにつれて価格がさがってきましたよね。したがって独占企業の場合の総収入は、このケースでは
TR=(100-Q)・Q=100Q-Q2
となります。ここでTRはTotal Revenue(総収入)です。横軸に数量、縦軸に総収入をとってグラフを書いてみてくださいね。山の形になりますから。
独占企業の場合も企業は、利潤を最大化するように生産量を決定すると考えます。利潤は
利潤=総収入−総費用
で得られます。だから、総収入に加えて、費用の構造が企業の利潤に大きな影響を与えます。この式の利潤をπ、総収入TR、総費用TCとすると
π=TR-TC
ですね。完全競争市場における利潤最大化と同様に、独占企業の場合も微分を使えば簡単に利潤最大化の必要条件を求めることができます。すなわちこの式を数量で微分して、ゼロとおけばよいわけです。つまり
dπ/dQ=d(TR)/dQ−d(TC)/dQ=0
限界収入−限界費用=0
限界収入=限界費用
となります。実は、完全競争市場における利潤最大化条件 価格=限界費用 もこの条件を満たしています。完全競争市場では、総収入=pQなので、Qで微分して限界収入を求めるとPになるからです。
いま、独占企業の費用関数が
TC=2Q+10
という式であらわされるとしましょう。独占企業が利潤を最大化するような最適な生産量はいくらになるでしょうか。この問題は、限界収入=限界費用という条件さえ暗記しておけば簡単に解くことができます。もっとも微分ができないと解けませんが・・・。
まず限界収入は、総収入を数量で微分すればよいので、独占企業の総収入TR=100Q-Q2をQで微分すると
d(TR)/dQ=100-2Q
になります。次に限界収入は、費用関数TC=2Q+10を数量Qで微分すると
d(TC)/dQ=2
になります。限界収入=限界費用なので
100-2Q=2
2Q=98
Q=49
になります。理解を深めるために縦軸に限界収入、限界費用、横軸に数量をとって、グラフを書いてみてくださいね。
とまとめることができます。日本全体で考えると企業が生産して発生した所得は、労働者への賃金、資本家への利潤の分配など誰かのものになります。だからまず、生産面でみたGNPと分配面でみたGNPが等しくなります。次に分配された所得は、家計が消費として使うか企業が投資として使うか、政府が使います。なお、生産したものを外国で販売する場合や、外国の商品を購入することもありますから外国貿易を考慮するときは、輸出と輸入のことも考えないといけません。でも財政学のテキストでは、簡単化のために、世界には日本しかないと想定して議論するので輸出と輸入は無視しています。これは閉鎖経済の仮定とよばれます。ここでもこの閉鎖経済の仮定をおいておきましょう。
以上の概念をよく覚えておいてください。あとで使いますから・・・
この需要の波及プロセスを整理してみましょう。
100億円+80億円(0.8×100)+64億円(0.8×0.8×100)+・・・・・
という風に当初の需要100億円が小さくなりながらも波及していきます。この波及した需要は派生需要とよばれます。この派生需要は、どこまでも続いていきます。すると最終的にはこの派生需要を合計するとどのぐらいの大きさになるのでしょうか。これは、波及プロセスを数式で表記することで解くことができます。
当初の需要増大の100億円を記号Aで置き換えます。次に、限界消費性向0.8は記号bで置き換えましょう。派生需要の合計額は
| 1990年 | 1991年 | 1992年 | 1993年 | 1994年 | 1995年 | 1996年 | |
| 所得 | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
| 消費 | 90 | 140 | 130 | 200 | 210 | 240 | 300 |
L=kY+(g−hr) (19) 貨幣需要関数
ここで、k、g、hは任意の定数です。kYの部分は、国民所得に一定割合kをかけたものが取引動機による貨幣需要と考えられることを示しています。g−hrの部分は、投機的動機による貨幣需要の部分を意味しています。 gは利子率に依存しない独立的な投資の部分、
-hrの部分は利子率が上昇するにつれて投機的な貨幣需要が減少することを意味しています。
貨幣市場における均衡は、この2つの式を同時にみたすような所得と利子率の組み合わせとして示されます。(18)式に(19)式を代入すれば
M=kY+(g−hr)
となります。次に左辺にrの項を移項し、Mを右辺に移項すると
hr=kY-M+g
となります。両辺をhで割ると
k (M-g)
r=----Y − ------ (20) LM曲線
h h
となります。この式はLM曲線と呼ばれます。すなわちLM曲線とは、貨幣市場を均衡させるような国民所得と利子率の組み合わせを意味します。
(3)財市場と貨幣市場の同時均衡
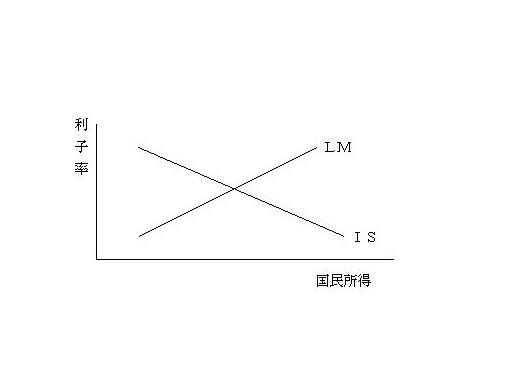
このようにして求めたIS曲線とLM曲線を縦軸に利子率、 横軸に国民所得をとってグラフに描くと上のようにIS曲線は右下がりの曲線、LM曲線は右上がりの曲線として描かれます。このIS曲線とLM曲線の交点では、財市場と貨幣市場が同時に均衡しています。この交点を垂直におろしたところが、均衡国民所得、水平に縦軸までのばした水準が均衡利子率となります。
それでは、均衡国民所得の水準を具体的に求めてみましょう。均衡国民所得の水準は、IS曲線とLM曲線の交点から求められるので
(17)式と(18)式において右辺同士を等しいとおくことで求まります。つまり
-(1-b) a+d+G k (M-g)
------Y+--------- =---Y - --------
e e h h
となります。このままではややこしいので、両辺にeをかけてみましょう。
-(1-b)Y+a+d+G =(ek/h)Y - e(M-g)/h
となります。少しすっきりしましたね。右辺にYの項を集めて、左辺にはYのついていない項を集めてみましょう。
a+d+G+e(M-g)/h=(1-b)Y+(ek/h)Y
右辺をYでくくると
a+d+G+e(M-g)/h={(1-b)+ek/h}Y
左辺と右辺を入れ替えると
{(1-b)+ek/h}Y= a+d+G+e(M-g)/h
となります。そこで両辺に1/{(1-b)+ek/h}をかけると
1
Y=-----------[ a+d+G+e(M-g)/h] 均衡国民所得の決定式
(1-b)+ek/h
となります。これが、財市場と貨幣市場を同時に均衡させるような均衡国民所得の決定式です。少し複雑な形をしてますが、一番シンプルなケースの均衡国民所得の決定式(6)式と比較してみてください。どことなく似てますね・・・。貨幣市場を考慮にいれたので多少ややこしくなってます。そのかわりこの式を使えば、財政政策たとえば政府支出Gを増やすような政策だけでなく、金融政策たとえば貨幣供給Mを増加させるような政策の効果をみることができます。
最近では、財政学の分野でも長期的な視野から分析の必要性が認識されるようになってきました。小泉改革の掲げる構造改革も短期的には痛みを感じる政策も長期的にみると日本経済の活性化につながるとされています。そこで、ここでは経済成長論のエッセンスを簡潔に説明しておきたいと思います。なお、経済成長論はマクロ経済学、ミクロ経済学の基礎知識がないと理解不能です。さらに、時間の概念を導入するために微分方程式、差分方程式といった高度な数学技法が要求されます。これらの前提条件をクリアしていない学力の学生さん履修しないほうが無難ですから・・・
1.投資理論
(1)投資の2重性
投資は、経済成長論において重要な役割を演じます。平成不況のなかで、日銀は低金利政策を採っていますよね。金利が低ければ、企業がお金を借りやすくなるので、投資が増えると考えられるからです。投資が増えれば、乗数効果を通じて国民所得が増加するということでしたよね。
国民所得の増加分=投資乗数×投資の増加分
という関係を覚えていますか。単純なケインズモデルの場合、投資乗数は1/(1−限界消費性向)で表されるのでしたよね。限界消費性向は、追加的に所得が増えたときに追加的に消費がどの程度ふえるかを示した比率です。1から限界消費性向を引いたものは、限界貯蓄性向と呼びます。所得のうち消費に回した残りは貯蓄することになりますから。上の関係を記号に置き換えましょう。国民所得をY、投資をI、増加分をΔ、限界貯蓄性向をsとすると
ΔY=(1/s)ΔI (1)
となります。
投資のもうひとつの効果が、資本ストックの付加による生産力創出効果です。ミクロ経済学で習った生産関数は資本と労働に依存してましたよね。資本ストックが増加すれば、生産関数を通じて生産力が増加するということになります。直感的に説明すると、トヨタが設備投資を増加させて、自動車工場に新たな生産ラインをつくれば生産台数の増加につながるというところですね。投資と資本の関係を記号で説明すると、資本をKとおくとき、
I=ΔK=Kt-Kt-1 (2)
となります。投資は資本の増加分と定義できます。増加分ですから、任意のt期とt-1期の資本の差額として記述することもできます。
さて、この投資が資本の付加を通じて生産力に与える効果も数式で表示してみましょう。
ΔY・v=ΔK (3)
この式は生産力の増加分の一定割合は、資本の増加によって生じたものだということを主張しているにすぎません。ここでvは、(限界)資本係数と呼ばれます。この式を書き換えると
ΔY=(1/v)ΔK (4)
となります。(3)式は、(2)式の関係を使うと
ΔY=(1/v)I (5)
とも書けます。
(2)加速度原理
加速度原理とは、投資の増大が、乗数効果を通じて生産量の増大を招き、生産量の増大は(3)式(あるいは(5)式)のような関係が成立すると考えればさらなる投資の増大を生じることになるという考え方です。直感的に説明すれば、トヨタが新しい生産ラインをつくれば、GNPが何倍かに増大する。なぜかというとトヨタの生産ラインの新設は、富士通ファナックのロボットの需要を増加させたり、その他の部品メーカの需要の増大など波及需要を生じると考えられるからです。波及需要を合計しただけ国民所得が増加し、その増加に見合った分だけ、トヨタは生産設備をさらに増大させると考えられるわけです。
(3)式のΔKを(2)式を利用して書き換えると、
ΔY・v=I
右辺と左辺を入れ替えると
I=v・ΔY
となります。ΔYはt期のt-1期のYの差額と表記できますから
I=v(Yt-Yt-1) (6) 加速度原理
と表記できます。要するに、加速度原理は、投資は所得の変化分の一定比率として説明できるという仮説です。正しいかどうかは別として・・・
2.景気循環論
経済成長率をグラフに採って調べてみると、不況と好況が交互に繰り返されてきたことがわかります。わが国でも円高不況、バブル、平成不況というように、景気は変動してきてますね。この景気の変動は、どのように説明できるかを昔から数多くの経済学者がさまざまな説明を試みてきています。以下では代表的なモデルのエッセンスのみを紹介しておきます。系統だった説明をする力量は、門外漢の私にはありませんので、本格的に腰を据えて勉強したい人は、経済成長論やマクロ経済学の上級のテキストを購入してくださいね。
(1)サミュエルソン・モデル
サミュエル・モデルは、ケインズの乗数理論と加速度原理を組み合わせて、景気の変動を説明しようとするものです。
所得の定義式を覚えていますか。Y=C+I+Gでしたよね。この関係式に時間の概念を入れて
Yt=Ct+It+G0 (7)
としましょうか。時間の添え字を付けただけですから、この式の意味自体は所得が消費需要、民間投資、政府投資に等しくなるというおなじみの話しと同じです。なお、Gだけ添え字をゼロとおいてますけど、これは政府支出は外生的に与えられて、時間をじて一定だと仮定するためです。次に消費関数ですけど、ケインズの消費関数は、C=a+bYという形でしたよね。でも、サミュエルソンモデルでは、少し違います。消費は、所得の関数と考えるところは同じなんですけど、「前期」の所得の関数だと考えます。今年の消費をおこなう場合、その期の所得でなく去年の所得に依存にして決まるとサミュエルソンは考えたわけですね。でもリストラされた人が去年の所得に依存して消費を決めたりすると困るでしょうね・・・。とりあえず、この仮定を受け入れたとして、さらに単純化のため消費は、前期の所得に単純に比例して決まるとしましょう。すると消費関数は
Ct=bYt-1 (0<b<1) (8)
としましょう。ここでbは限界消費性向であり、正の定数です。次に投資は、消費の増加量の関数だとしましょう。この関係を式で表記すると
I=v(Ct−Ct-1) (v>0) (9)
となります。ここで、(8)式を(9)式に代入してみましょう。
I=v(bYt-1−bYt-2)
=vb(Yt-1−Yt-2) (10)
次に、(10)式と(8)式を所得の定義式(7)式に代入しましょうか。
Yt=bYt-1+vb(Yt-1−Yt-2)+G0
Yt=bYt-1+vbYt-1−vbYt-2+G0
Yt=(1+v)bYt-1−vbYt-2+G0 (11)
(11)式は、t期の所得は、t-1期の所得とt-2期の所得そして外生的に与えられる政府支出に依存して決まるということを示した2階の差分方程式です。この式は景気の変動が、加速度係数vと限界消費性向bに依存して決まることを示しています。このvとbの2つの定数の値が決まれば、所得Yの経路を描くことができるのですけど、それには高度な数学的な技法が要求されます。数学が苦手な人は、吉川洋『現代経済学 マクロ経済学』岩波書店に、非常にわかりやすい説明が載っていますのでそれを読んでください。数学が得意な人は、チャン著大住・小田・高森・堀江訳『現代経済学の数学的基礎(下)』の説明をご覧ください。
(2)ヒックス・モデル
ヒックス・モデルも、景気の循環を加速度原理と乗数理論を組み合わせたものです。具体的には
消費関数 Ct=(1-s)Yt-1 (12)
加速度原理 It=v(Yt-1-Yt-2) (13)
独立投資 At=(1+g)tA0 (14)
という方程式体系を利用します。ただしsは限界貯蓄性向です。Aoは初期時点の独立投資であり、独立投資は毎期gの割合で成長するものと仮定されます。消費と投資を足したものは所得に等しくなると考えられますので、t期において
Yt=Ct+It+At (15)
が成立します。(15)式に(12)(13)(14)式を代入すると、最終的に
Yt=(1-s+v)Yt-1−vYt-2+(1+g)tA0 (16)
というような2階の差分方程式になります。この式は、t期の所得は、t−1期の所得、t−2期の所得に依存して決まること、さらに独立投資にも依存していることを表しています。このヒックスモデルの特徴は(16)式で示される差分方程式で描写される景気循環は、「上方限界」と「下方限界」の間で、所得水準が上昇と下降を繰り返すことです。ヒックスモデルは、最近のマクロ経済学のテキストではまず説明されることはありません。現在の経済成長論は、ミクロ的な基礎を持ったものに移行してしまったためです。したがって、あえてこのモデルを学ぶ必要性は一般の学生さんにはないと思います。ただし、公務員試験の問題集にはまだ載っています。実際に公務員試験に出題されるかどうかはわかりません。試験委員が世代交代していけばまずでないでしょうけど・・・
3.経済成長論
景気循環論としてのサミュエルソン・モデルやヒックス・モデルが好況と不況を繰り返す景気循環の仕組みを明らかにしようとしたものであったのに対して、経済成長論は、経済成長のメカニズムを明らかにしようとするものです。
(1)ハロッドの成長論
経済成長論における最初の理論的な貢献は、ハロッドの論文だと言われています。ハロッドのモデルは、同時期に同様のモデルを開発したドーマーのモデルと合わせて、ハロッド・ドーマーの経済成長モデルと呼ばれています。この両者の比較を知りたい人は、ハイウェルG.ジョーンズ、松下訳『現代経済成長理論』をご覧下さい。そのあたりの高尚な話しは棚にあげておくとして、ハロッドモデルは以下のように説明できます。まずは、ハロッドモデルでは、投資の効果として資本ストックによる生産力創出効果を想定します。
資本ストックをK、産出量をYとしたとき、
K=vY (v>0) (12)
が成立するとしましょう。投資は資本ストックの変化分ですからI=ΔKという関係が成立します。このKに(12)式を代入すると
I=vΔY (13)
となり、これは(6)式の「加速度原理」による投資の決定を表していることがわかります。
次に消費関数を単純化のため、国民所得Yの一定割合だとします。つまり
C=bY (14)
だとします。ここで、bは限界消費性向です。国民所得の定義式において政府支出を無視すると
Y=C+I (15)
が成立します。(15)式に(14)式を代入すると
Y=bY+I
Y=I/(1−b)
Y=I/s (16)
となります。ここでsは限界貯蓄性向ですね。(16)式と(13)式から
I=vΔY=sY
となるので
ΔY/Y=s/v (17)
が成立します。つまり成長率は、s/vで与えられます。ハロッドはこの成長率を保証(ないし適正)成長率(warranted
rate of growth)と呼びました。保証成長率と呼ぶのは、これが資本の完全雇用を実現する成長率となっているからです。
保証成長率に加えて、ハロッドは自然成長率という概念を導入しました。これは、労働の完全雇用を実現する成長率であり、人口成長率nに等しくなります。労働をLとして、人口成長率をnとおくと
ΔL/L=n
と表記されます。経済成長率は人口成長率より低いと、初期時点で完全雇用の状態にあるとき、新たに労働市場に参加する人の職が確保されないことになりますから。したがって、経済が資本と労働の完全雇用を達成しながら成長するためには、保証成長率と人口成長率が一致しなければなりません。
これがたまたま、一致すればよいのですが、これらの値が一致する保証はありません。もし現実の成長率が保証成長率よりも高い場合には、資本が不足することになってしまいます。すると企業は投資をこれまでも増加させようとします。投資を増やすと現実の経済成長率はさらに上昇するので、現実の成長率と保証成長率の乖離はさらに拡大してしまいます。逆に、現実の成長率が保証成長率よりも低いときには、資本が過剰になり企業が投資を控えるので現実の成長率はさらに低下し、やはり現実の成長率と保証成長率の乖離が拡大していきます。このようにハロッドは、経済成長率はひとたび均衡をはずれるともとの状態に回復しないという非常に不安定な性質を持つとしました。この性質は「ナイフエッジ定理」と呼ばれています。
(2)ソロー・モデル
ハロッドの経済成長モデルが、一度均衡をはずれるともとの状態に回復しないという非常に不安定な性質を持っているのに対して、ソローに代表される新古典派の経済成長理論では、安定的な性質を持っています。ソロー・モデルは、ハロッドモデルと異なり、ミクロ経済学の考え方に時間の概念を導入して発展させたものです。ミクロ経済学において、企業は資本と労働という生産要素を投入して、生産をおこなうという生産関数を想定することを覚えていますか。生産量をY、資本をK、労働をLとおくと、生産関数は一般的に
生産関数 Y=F(K,L) (18)
と表記できます。この生産関数に関して、規模に関して収穫一定という性質が成立するとしましょう。規模に関して収穫一定とは、K、Lという生産要素がすべてN倍になったとすると、生産量もN倍になるということを意味しています。N倍以上に生産量が増大するときは、規模に関して収穫逓増、逆にN倍以下のときは規模に関して収穫逓減と呼びます。現実の企業は、必ずしも規模に関する収穫一定の生産関数を持っているわけではありません。たとえば、マイクロソフトのようにパソコンのソフトウェアの場合には、一度シェアを奪ってしまうとみんながそのソフトを使わざるをえなくなり、規模に関して収穫逓増が成立するとも言われています。しかし、ミクロ経済学の世界では、分析が単純化できるため、規模に関して収穫一定という仮定がしばしば置かれます。学部レベルでは覚える必要はないですが、大学院生にとっては必須のテクニックですから。
規模に関して収穫一定を仮定すると、(18)式は一人あたりの生産関数に置き換えることができます。
y=f(k) (19)
ここで、yはY/L、kはK/L、資本労働比率(capital labor ratio)です。
ソローモデルでも、投資は経済成長に大きな役割を果たします。また投資と貯蓄は等しくなるので貯蓄もまた重要な意味を持ちます。貯蓄に関しては、ソローモデルは、所得の一定比率だと仮定します。すなわち、所得をY、限界貯蓄性向をsとおくと
貯蓄関数 S=sY 0<s<1 (20)
となります。次に投資と資本の間の関係には
ΔK=I (21)
が成立します。ここでΔK=dK/dt、つまり資本を時間tで微分したものとします。(時間の微分は経済学のテキストでは変数の上にドットをつけて表現するのですけど、HTMLでドットを出す方法がわからないもので・・・。)資本の増加分は投資に等しいと考えます。なお、この式では単純化のため資本減耗を無視していますけど、通常は資本は少しずつ価値が減っていくものとされます。投資は貯蓄と等しいので(21)と(20)から
ΔK=S=sY (22)
が成立します。次に労働力(人口)Lは外生的に一定の割合nで成長すると仮定しましょう。つまり、
ΔL/L=n (23)
とします。
次に、所得の定義式を思い出しましょう。政府部門と外国貿易を無視すると
Y=C+I (24)
ですね。(24)式の両辺をLで割ると
Y/L=C/L+I/L
となります。この式の左辺は、一人あたりの産出量yに置き換えることができます。
f(k)=C/L+I/L (25)
この式では、煩雑化を避けるために時間の添え字を省略していますが、この式は任意の期間tについて成立します。次に資本労働比率kの成長率を定義します。資本労働比率は、資本を労働で割ったものです。もし、資本と労働が同じ割合で増加するならば資本の増加分、労働の増加分ともにゼロとなり、資本労働比率kの成長率もゼロになります。資本の増加割合が労働の増加割り合いより大きいときは、k>0となり、資本の増加割合が労働の増加割合よりも小さければk<0になりますね。数学的にはkの成長率は、時間tで微分すれば求まります。つまり
dk/dt=d(K/L)/dt=(ΔKL−KΔL)/L2 (25)
ですね。KとLはそれぞれ時間tの関数です。分数の形になっているので商の微分公式を使います。商の微分公式については高校の数学の本か経済数学のテキストをみてください。(25)式を整理すると
dk/dt=Δk=ΔK/L−(ΔL/L)k (26)
になります。両辺に1/kをかけると
Δk/k=ΔK/K−ΔL/L (27)
が求まります。この式は、資本労働比率の成長率は、資本の成長率から労働の成長率を差し引いたものと等しくなることを意味しています。この(27)式に(23)式を代入すると
Δk/k=ΔK/K−n (28)
となります。ここで両辺にkをかけると
Δk=(ΔK/K)・k−nk
となります。ΔK=sYをこの式に代入すると
Δk=s(Y/K)(K/L)−nk
=sy−nk
ですね。一人あたりの生産関数(19)式を使うと
Δk=sf(k)−nk (29)
が得られます。(29)式がソローモデルにおける基本方程式です。
つづきはそのうちに
![]()
Copyright(c) 1999 by Kyoji Hashimoto
Last Updated 2001/07/24 20:14:28