8.1 課税の効率性
(1)超過負担
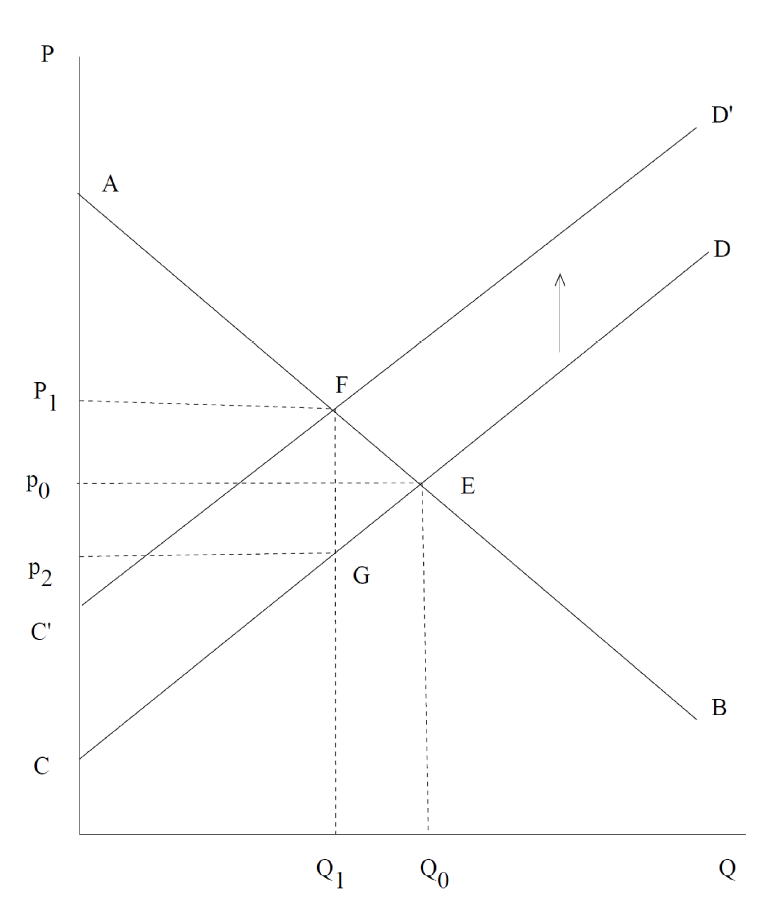
図8-1 課税の超過負担
消費者余剰:消費者が支払ってもよいと考える価格と実際に支払う価格の差
生産者余剰:生産者が売ってもよいと考える価格と実際に受け取る価格の差
総余剰=消費者余剰+生産者余剰
超過負担 三角形 EFG
(2)一般消費税と個別消費税
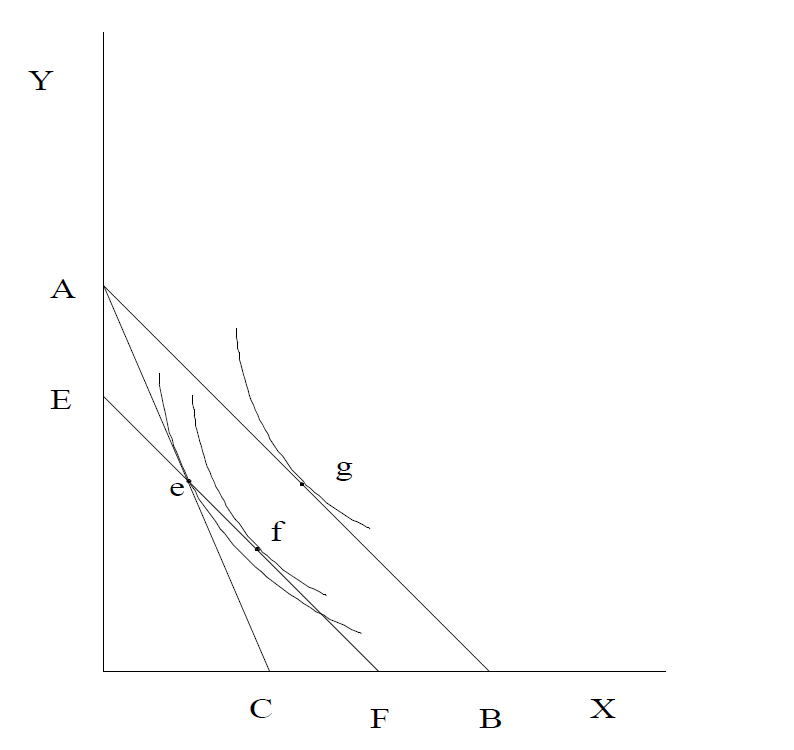
図6−2 一般消費税と個別消費税の比較
一般消費税の方が同じ税収のもとでより高い効用水準を達成することができる。
→一般消費税はランプサムタックスと同様に所得効果のみを生じている
↓
社会にはX財とY財の2財しか存在しないという単純化の仮定をおいたため
現実には、一般消費税は余暇に課税していないという意味で、すべての財に課税しておらず、超過負担を発生させることになる。
ラムゼー・ルール(逆弾力性命題)
需要の価格弾力性が大きい財(奢侈品、嗜好品) 課税による超過負担が大きいので軽課
需要の価格弾力性が小さい財(必需品) 課税による超過負担が小さいので重課
複数家計が存在する場合の最適課税ルール
→低所得者の需要が相対的に多い財については低い税率で課税すべき
(大阪大学財政研究会編『現代財政』創文社,1985年10月参照)
8.2 ライフサイクル・モデル
(1)労働所得税と消費税の等値性
(旧)政府税制調査会
「財貨・サービスの消費に幅広く等しく負担を求める性格から、勤労世代など特定の者への負担が集中せず、
その簡素な仕組みともあいまって貯蓄や投資を含む経済活動に与える歪みが小さいという特徴を有する。」
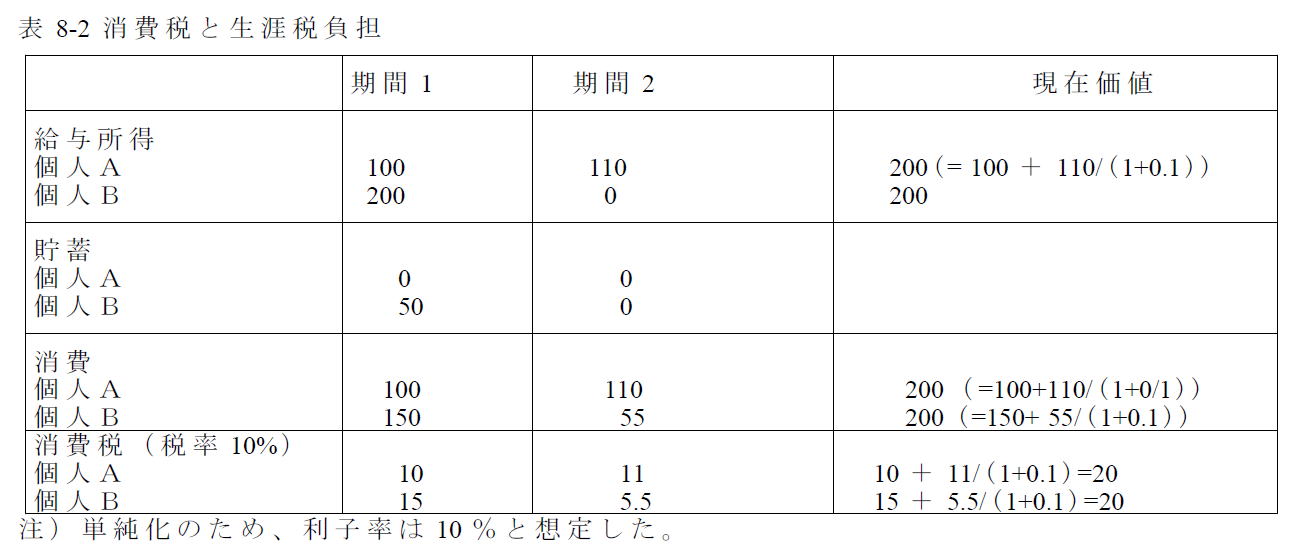
単純なライフサイクル・モデルにおいては、労働所得税(賃金税)と消費税の間には等値性が成立する
2期間のライフサイクルモデルによる等値性の証明
第1期は、勤労期間で、第2期は退職後の期間とする。
第1期には、所得を獲得して、その1部を消費し、残りを2期めの消費のために貯蓄する。
2期目は退職後のため、1期目の貯蓄とその貯蓄から生じた利子所得を消費する。
この人は、死ぬまでに貯蓄はすべて消費してしまうと仮定する。
まず、所得をY、1期の消費をC1、貯蓄をSとおくと、第1期の予算制約は、
Y-C1=S (8-1)
となる。
次に、第2期の消費をC2、利子率をrとすると、第2期の予算制約は、
C2=(1+r)S (8-2)
となる。
(8-2)式の右辺のSに(8-1)式の左辺を代入すると
C2=(1+r)(Y -C1)
となる。両辺を(1+r)で割り算すると
C2/(1+r)=Y-C1
となる。右辺のC1を左辺に移項すると
C1+C2/(1+r)=Y (8-3) 生涯の予算制約式
となる。
(2)労働所得税と消費税の比較
消費税の税率をτ、労働所得税の税率をtとする。
消費税課税後の生涯の予算制約式は
(1+τ)C1+(1+τ)C2/(1+r)=Y (8-4)
となる。
労働所得税課税後の予算制約式は、
C1+C2/(1+r)=(1-t)Y (8-5)
となる。この2つの生涯の予算制約式は、消費税と所得税の税率の関係を適切に設定することで全く同じものとなる。
(8-4)式の両辺を(1+τ)で除すると、
C1+C2/(1+r)=1/(1-τ)Y (8-6)
となる。ここで(1-t)=1/(1-τ)が成立する場合には、(8-6)式と(8-5)式は完全に一致することになる。
消費税と労働所得税の等値性は、現実の世界では成立しない理由
1.一般均衡分析では必ずしも労働所得税と消費税の等値性は成立しない。
井堀(1984)は「青年期の所得だけにかかる労働所得税と、青年期、老年期両方にかかる消費税では、
貯蓄に与える影響が異なり、したがって、要素価格に及ぼす効果にも差が生じる。
経済全体の均衡を考える一般的均衡分析では消費税と労働所得税は等値ではなく、
それぞれの最適値は一意的に定まる」
2.移行期を考慮した世代重複モデルを想定すると、労働所得税と消費税の影響は世代によって全く異なる。
ある時点で、所得税から労働所得税へ切り替わるという税制改革を想定した場合、
すでに労働所得税のもとで課税されてきた世代は、消費税への移行に伴い、
若年期での労働所得税と老年期での消費税の双方を負担するのに対して、
これから労働市場に参入する世代は、労働所得税を負担せず、消費税のみを負担することになる。
3.職種の異なる複数家計の存在を考慮すると等値性は成立しない。
親からの莫大な遺産から生じる資産所得のみで、生涯を通じて全く働くことなく暮らせる家計と勤労者の双方を考慮した場合
→消費税であれば両者に課税することができる
(3)利子所得税と消費税の比較
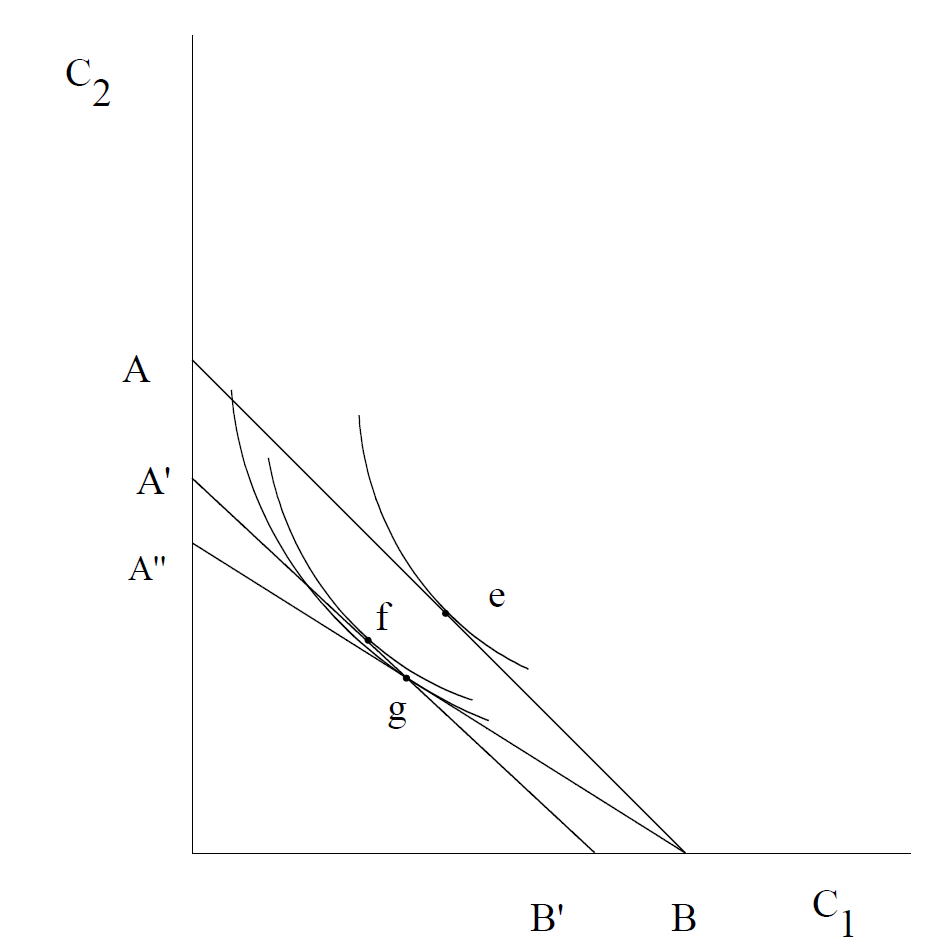
図8−3 利子所得税と消費税の比較
利子に対する比例税率をθとすると、課税後の予算制約式は、
C1+C2/{1+(1-θ)r}=Y (8-7)
となる。この式のC1を移項すると
C2/{1+(1-θ)r}=−C1 + Y
となる。両辺に{1+(1-θ)r}を乗じると
C2=−{1+(1-θ)r}C1 +{1+(1-θ)r}Y (8-8)
となる。この式は、切片が{1+(1-θ)r}Y、傾きが−{1+(1-θ)r}の一次関数となっている。同様にして、消費税課税後の予算制約式は、
C2= −(1+r)C1+(1+r)Y /(1+τ) (8-9)
と変形できる。
(8-8)式 利子所得税を増税した場合には、この予算制約式のグラフが回転
(8-9)式 消費税を増税した場合には、傾きは不変で切片のみが減少する
同じ税収のもとで消費税のほうが利子所得税よりも高い効用水準を達成することができる。