( 変更履歴:
v0.2 [11/10/30] f2cの計算式を変更しました。)
Wave信号を合成してみます。
function makeWave(key, multi)
sf = 44100; # サンプリング周波数
time = 2.0; # 時間・秒
n = fix(time*sf);
t = linspace(0, time, n);
omega = 2*pi*t;
mul = 1:multi; # 倍音数
f0 = getFrequ(key)*mul;
f = zeros(1,n);
for m = mul
f += sin(omega*f0(m))./multi;
end
wavwrite_f(f, sf, 16, 'test.wav');
end
function wavwrite_f(s, fs, bits, wavefile)
fid = fopen(wavefile, 'wb', 'ieee-le');
length_of_s = length(s);
if bits == 8
dataChunkSize=length_of_s;
elseif bits == 16
dataChunkSize=length_of_s*2;
end
RiffChunkID = 'RIFF';
RiffChunkSize = dataChunkSize+36 #
RiffFormType = 'WAVE';
fmtChunkID = 'fmt ';
fmtChunkSize = 16;
fmtWaveFormatType = 1;
fmtChannel = 1;
fmtSamplesPerSec = fs;
fmtBytesPerSec = fs*bits/8;
fmtBlockSize = bits/8;
fmtBitsPerSample = bits;
dataChunkID = 'data';
% 'RIFF' chunk
fwrite(fid,RiffChunkID,'uchar');
fwrite(fid,RiffChunkSize,'uint32');
fwrite(fid,RiffFormType,'uchar');
% 'fmt ' chunk
fwrite(fid,fmtChunkID,'uchar');
fwrite(fid,fmtChunkSize,'uint32');
fwrite(fid,fmtWaveFormatType,'uint16');
fwrite(fid,fmtChannel,'uint16');
fwrite(fid,fmtSamplesPerSec,'uint32');
fwrite(fid,fmtBytesPerSec,'uint32');
fwrite(fid,fmtBlockSize,'uint16');
fwrite(fid,fmtBitsPerSample,'uint16');
% 'data' chunck
fwrite(fid,dataChunkID,'uchar');
fwrite(fid,dataChunkSize,'uint32');
if bits==8
s = round((s+1)*255/2);
fwrite(fid,s,'uchar');
elseif bits==16
s = round((s+1)*65535/2)-32768;
fwrite(fid,s,'int16');
end
fclose(fid);
end
wavwrite_f.mは Octaveにある wavwrite.mを改造したものです。
(参考文献:「ディジタル・サウンド処理入門」
青木 直史:著 CQ出版 2006年)
> makeWave(37, 5)
始めは 平均律です。
キー番号 37A・5倍音までの test.wavを作成します。
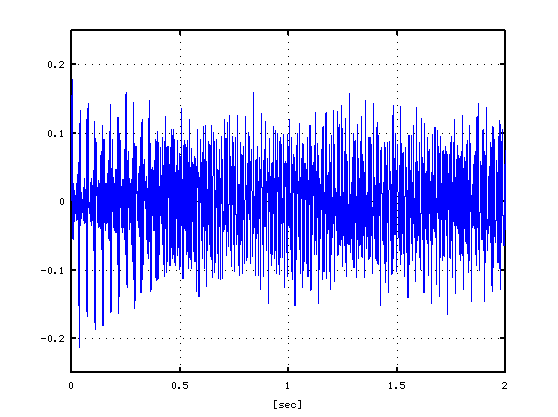
減衰しない 2秒間の Wave信号です。
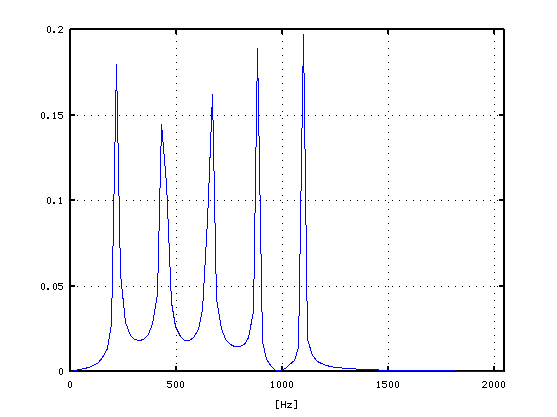
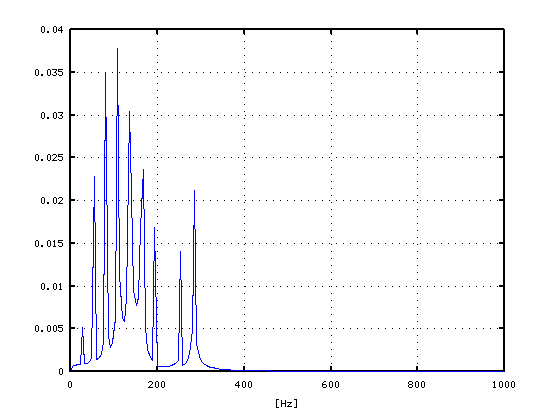
その FFTスペクトルです。
ではまず 打弦点の特性を作ります。
function val = stPoint(multi, sp) mp = multi.*pi; val = abs(sin(mp.*sp)./mp); end
> sp = stPoint(1:25, 1/8) > stem(sp, '-@') > grid on
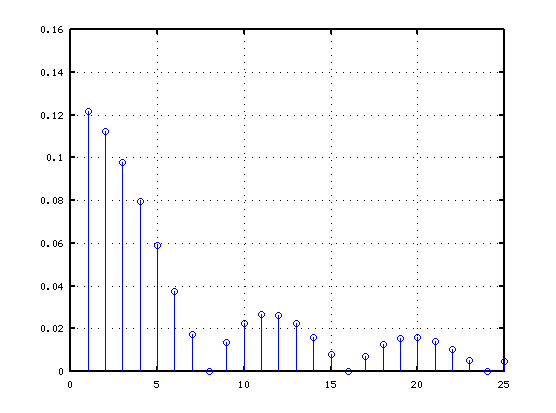
打弦点 1/8で 25倍音までです。
響板の振動特性を作ります。
実際は 凸凹のある特性ですが
ここではシミュレーションと云う事で フラットとしています。
function gain = kyoban(freq)
cutoff = 20; # 最下限周波数
band = 170; # 減衰幅
freq -= cutoff;
gain = freq/band;
if (gain < 0)
gain = 0;
elseif (gain > 1.0)
gain = 1;
end
end
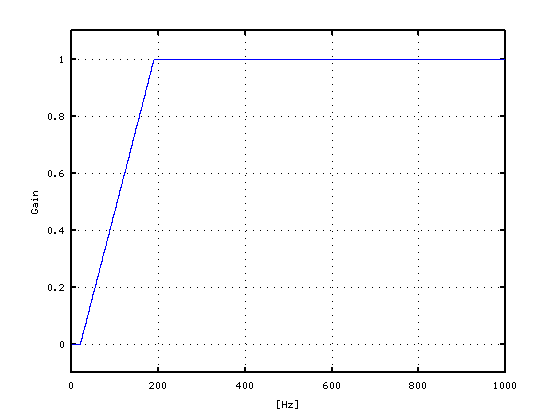
190[Hz]以下で減衰して 20[Hz]で 0になります。
> kyoban(200) ans = 1 > kyoban(150) ans = 0.76471 > kyoban(10) ans = 0
0から1000[Hz]までを見てみます。
キー毎の打弦位置を設定します。
function sp = strikP(key)
a49 = 8;
c88 = 22;
if (key > 49)
sa = 88-49+1;
points = logspace(log10(a49), log10(c88), sa);
sp = 1/points(key-48);
else
sp = 1/a49;
end
end
49Aまでは 1/8, 49Aから88Cまでは 1/8から 1/22へと変化させています。
> strikP(49) ans = 0.12500
以上に Tuningのシミュレーションを加えて
インハーモニシティのある Wave信号を作ります。
実際にピアノの音をシミュレーションするには
ハンマーの特性なども係わってきますが
取り合えず必要な倍音成分のみとしています。
function makeWave1(key, multi)
global Inha Cent KB;
KB = 88;
grade = 0.087; # 傾き
Inha = makeCurve(28, 0.55, grade);
Cent = tuning_c(Inha, 1.0, grade);
sf = 44100; # サンプリング周波数
time = 2.0; # 時間・秒
n = fix(time*sf);
t = linspace(0, time, n);
omega = 2*pi*t;
mul = 1:multi; # 倍音数
f0 = getIFrequ(key, mul);
sp = strikP(key);
f = zeros(1, n);
for m = mul
f += sin(omega*f0(m))*stPoint(m, sp)*kyoban(f0(m));
end
wavwrite_f(f,sf,16,'test.wav');
end
1Aキーで 10倍音までの Wave信号を作成します。
> makeWave1(1, 10)
その Wave信号です。
その FFTスペクトルです。
その Wave信号を検証してみます。
peaks.mは FFTと「補間公式」を使ってピークを検出します。
function ps = peaks(wave_file)
n = pow2(13); # サンプル数
n2 = n/2;
[s,fs] = wavread(wave_file);
delf = fs/n;
hn = hanning(n); # 窓関数
sx = s(1:n).*hn;
pks = abs(fft(sx,n)/n2); # FFT
maxkey = 88+12*3;
peak = zeros(maxkey,1);
for x = 2:n2-1
if (pks(x) > 0.0005) # クリッピング
if ((abs(pks(x)) >= abs(pks(x-1))) &\
(abs(pks(x)) >= abs(pks(x+1))))
bet = 3/(1+pks(x)/pks(x+1))-1;
frq = (x+bet)*delf-delf;
key = f2k(frq);
peak(key) = frq;
x += 2;
end
end
end
ps = peak(peak > 0);
end
function key = f2k(freq) key = round(12*log(freq/27.5)/log(2))+1; end
f2k.mは 周波数からキー番号を得ます。
> f2k([110.3 220.5 440.7]) ans = 25 37 49
makeWave1 で作った Wave信号からピークの周波数を取り出します。
> peaks('test.wav')
ans =
27.026
54.084
81.329
108.823
136.649
164.947
193.753
253.314
284.310
その周波数をセント値に変換して 補正値を加えて見てみます。
function f2pc(freq, malti)
Ladder = [0.0 0.0 -1.955 0.0 13.6863 -1.955 31.1741 0.0 -3.91 13.6863\
48.6821 -1.955 -40.5277 31.1741 11.7313 0.0 -4.9554 -3.91\
2.487 13.6863 -29.2191 -48.6821 28.2743 1.9550 -27.3726];
k = f2k(freq);
f = f2c(k, freq);
pcent = f'+Ladder(malti);
plot(malti, pcent, '-@;;')
grid on
end
function cent = f2c(key, freq) cent = 1200*log2(freq./getFrequ(key)); end # キー番号と周波数から cent値に変更します
> pk = peaks('test.wav')
> f2pc(pk, [1:7 9 10])
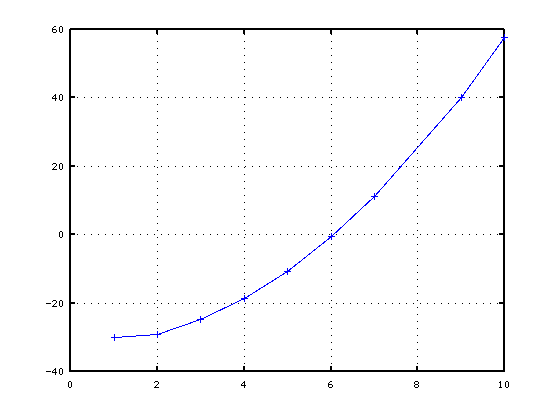
倍音が少しずつずれているのが分かると思います。
試しに peaks.mの以下の2行を
bet = 3/(1+pks(x)/pks(x+1))-1; frq = (x+bet)*delf-delf;
以下の1行のみに変更すると
frq = x*delf-delf;
「補間公式」を使わない FFTのみでの結果となります。
> peaks('test.wav')
ans =
26.917
53.833
80.750
107.666
134.583
166.882
193.799
253.015
285.315
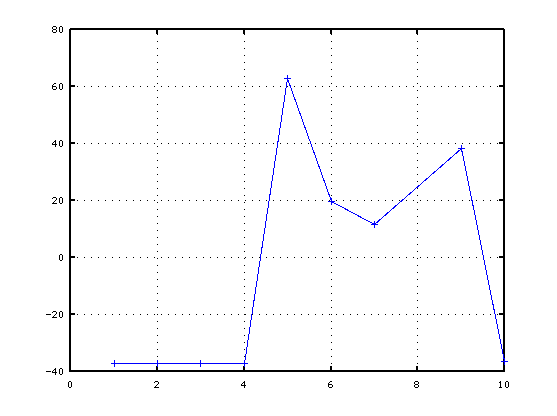
実際の信号から倍音列を検出するには その他にも計算が必要です。
参考文献: