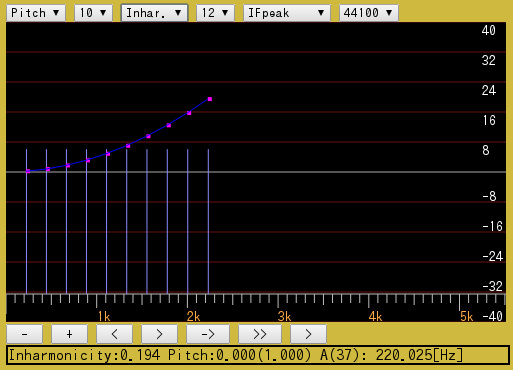
例えば A37キーの10倍音(平均律)を考えてみます。
倍数 : Key# : 周波数[Hz] : 差[cent] ----------------------------------- 1 : A(37) : 220.0000 : 0.0000 2 : A(49) : 440.0000 : 0.0000 3 : E(56) : 660.0000 : 1.9550 4 : A(61) : 880.0000 : 0.0000 5 : Cis(65) : 1100.0000 : -13.6863 6 : E(68) : 1320.0000 : 1.9550 7 : G(71) : 1540.0000 : -31.1741 8 : A(73) : 1760.0000 : 0.0000 9 : H(75) : 1980.0000 : 3.9100 10 : Cis(77) : 2200.0000 : -13.6863 -----------------------------------
それを Wave信号(サンプリング周波数は44100[Hz],2秒間)に合成して
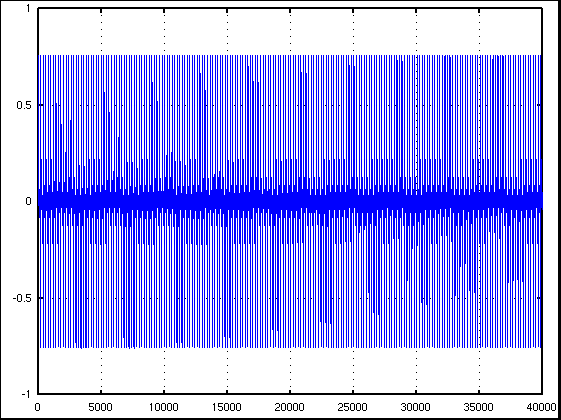
1. FFTで見てみます。
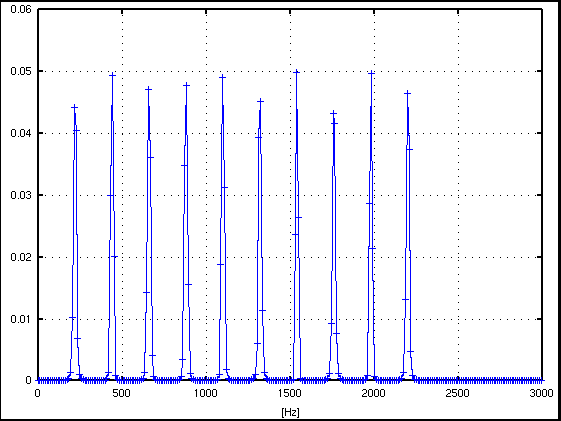
FFTのサンプル数は 4096=2^12です。 普通は上図の様に表示しますが 厳密(?)には下図の方が近いと思われます。
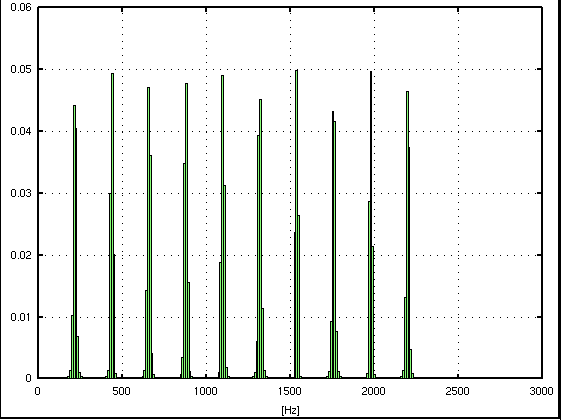
FFTには サンプリング周波数/サンプル数=分解能[Hz] と言う性質があります。 この場合は 44100/4096=10.767[Hz]で 上図の棒グラフの幅はそれを表しています。
では FFTのピークの周波数を表示してみます。
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 215.332 : -37.129: -37.129 : .... 2: A(49) : 441.431 : 5.620: 5.620 : 1.416 3: E(56) : 656.763 : -6.558: -8.513 : -0.941 4: A(61) : 882.861 : 5.620: 5.620 : 0.354 5: Cis(65) : 1098.193 : -16.532: -2.846 : -0.112 6: E(68) : 1324.292 : 7.575: 5.620 : 0.157 7: G(71) : 1539.624 : -31.597: -0.423 : -0.008 8: A(73) : 1754.956 : -4.969: -4.969 : -0.077 9: H(75) : 1981.055 : 4.832: 0.922 : 0.012 10: Cis(77) : 2196.387 : -16.532: -2.846 : -0.028 --------------------------------------------------
c.equalはキーの周波数との差です。 c.pureは補正値を加えた値です。 (I.const.はc.pureから計算したインハーモニシティ値です。) c.pureをグラフにしてみます。
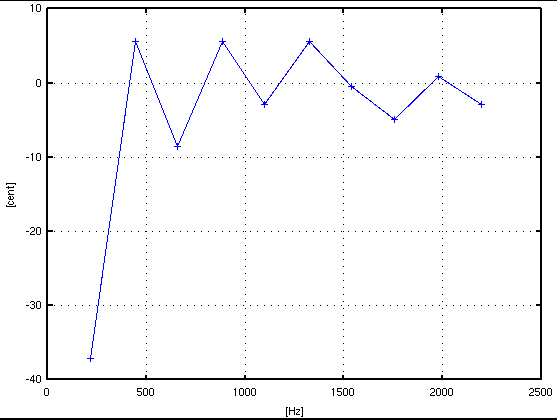
では解像度を上げてみたらどうでしょう? 8192=2^13の場合 44100/8192=5.383[Hz]です。
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 220.715 : 5.620: 5.620 : .... 2: A(49) : 441.431 : 5.620: 5.620 : 1.544 3: E(56) : 662.146 : 7.575: 5.620 : 0.686 4: A(61) : 877.478 : -4.969: -4.969 : -0.276 5: Cis(65) : 1098.193 : -16.532: -2.846 : -0.092 6: E(68) : 1318.909 : 0.523: -1.432 : -0.024 7: G(71) : 1539.624 : -31.597: -0.423 : 0.003 8: A(73) : 1760.339 : 0.334: 0.334 : 0.014 9: H(75) : 1981.055 : 4.832: 0.922 : 0.018 10: Cis(77) : 2201.770 : -12.294: 1.392 : 0.019 -------------------------------------------------
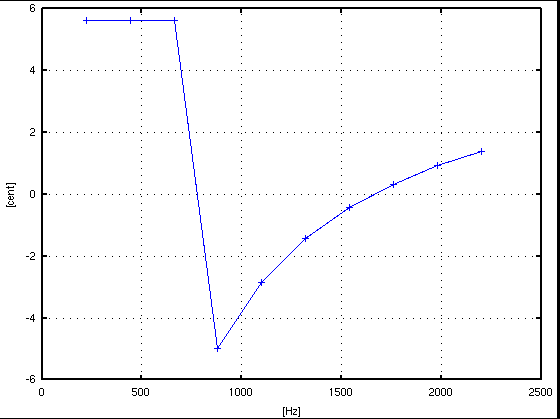
さらに解像度を上げて見ます。 16384=2^14の場合 44100/16384=2.691[Hz]です。
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 220.715 : 5.620: 5.620 : .... 2: A(49) : 438.739 : -4.969: -4.969 : -0.848 3: E(56) : 659.454 : 0.523: -1.432 : 0.016 4: A(61) : 880.170 : 0.334: 0.334 : 0.119 5: Cis(65) : 1100.885 : -12.294: 1.392 : 0.119 6: E(68) : 1318.909 : 0.523: -1.432 : 0.004 7: G(71) : 1539.624 : -31.597: -0.423 : 0.024 8: A(73) : 1760.339 : 0.334: 0.334 : 0.030 9: H(75) : 1981.055 : 4.832: 0.922 : 0.031 10: Cis(77) : 2199.078 : -14.412: -0.725 : 0.009 -------------------------------------------------
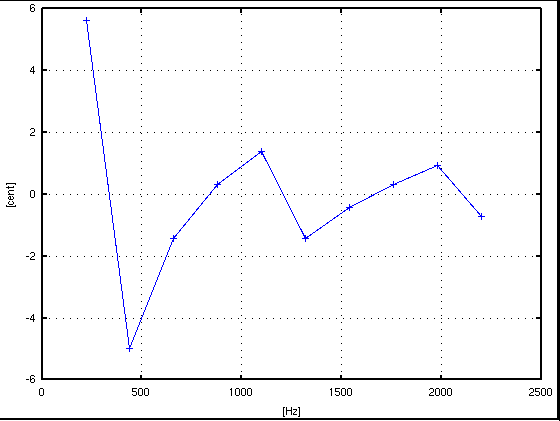
2. 「ピッチ抽出の試み (その1)(Pitch)」に ピークピッキング法(*1)と言うのがあります。
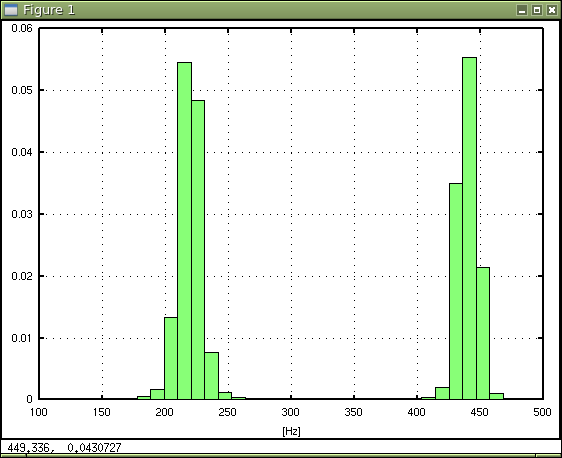
上の図の様な FFTのピークとその前後の値から 中心のピーク位置を得ようとする方法です。
A37です。サンプル数 = 4096(2^12),分解能 = 10.767[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 218.057 : -15.356: -15.356 : .... 2: A(49) : 441.323 : 5.197: 5.197 : 1.171 3: E(56) : 657.572 : -4.425: -6.380 : -0.766 4: A(61) : 882.300 : 4.518: 4.518 : 0.250 5: Cis(65) : 1098.383 : -16.233: -2.547 : -0.122 6: E(68) : 1322.391 : 5.089: 3.134 : 0.073 7: G(71) : 1539.629 : -31.591: -0.417 : -0.019 8: A(73) : 1758.799 : -1.182: -1.182 : -0.026 9: H(75) : 1980.998 : 4.782: 0.872 : 0.004 10: Cis(77) : 2197.498 : -15.656: -1.970 : -0.025 --------------------------------------------------
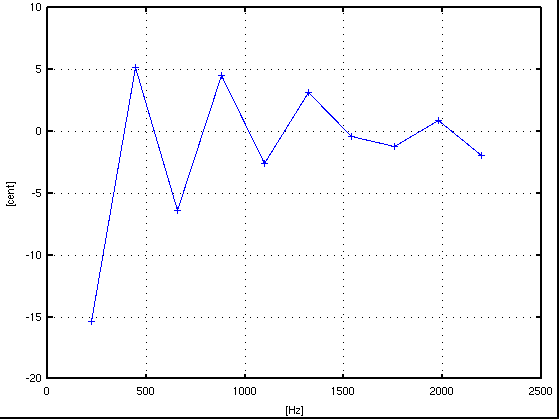
サンプル数 = 8192(2^13),分解能 = 5.383[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 220.659 : 5.180: 5.180 : .... 2: A(49) : 441.148 : 4.511: 4.511 : 1.162 3: E(56) : 661.195 : 5.086: 3.131 : 0.363 4: A(61) : 879.414 : -1.153: -1.153 : -0.064 5: Cis(65) : 1098.755 : -15.647: -1.960 : -0.073 6: E(68) : 1319.061 : 0.723: -1.232 : -0.030 7: G(71) : 1539.641 : -31.578: -0.404 : -0.005 8: A(73) : 1760.327 : 0.322: 0.322 : 0.007 9: H(75) : 1980.922 : 4.716: 0.806 : 0.012 10: Cis(77) : 2201.272 : -12.686: 1.001 : 0.011 -------------------------------------------------
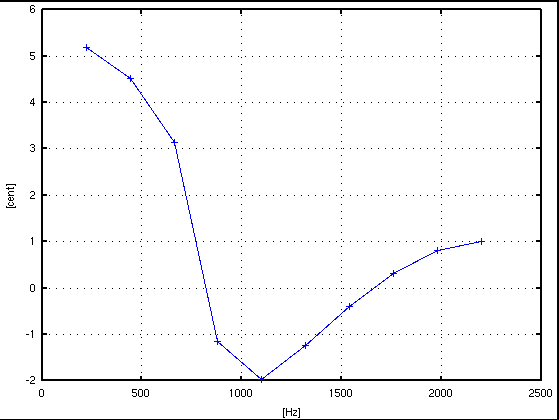
サンプル数 = 16384(2^14),分解能 = 2.692[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 220.571 : 4.490: 4.490 : .... 2: A(49) : 439.700 : -1.180: -1.180 : -0.170 3: E(56) : 659.530 : 0.721: -1.234 : -0.081 4: A(61) : 880.164 : 0.323: 0.323 : 0.052 5: Cis(65) : 1100.636 : -12.685: 1.001 : 0.060 6: E(68) : 1319.450 : 1.233: -0.722 : -0.006 7: G(71) : 1539.659 : -31.557: -0.383 : 0.002 8: A(73) : 1760.317 : 0.312: 0.312 : 0.013 9: H(75) : 1980.631 : 4.462: 0.552 : 0.013 10: Cis(77) : 2199.396 : -14.161: -0.475 : 0.000 -------------------------------------------------
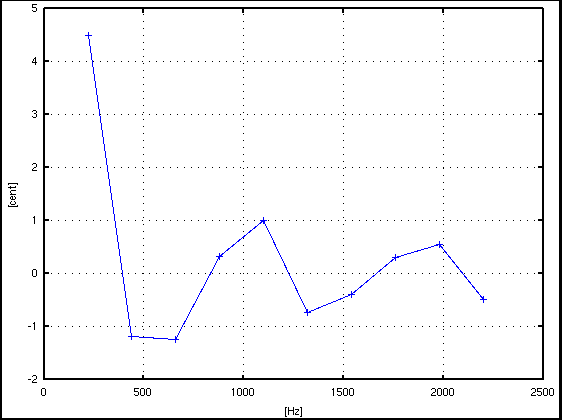
3. そして補間公式(*2)と言う FFTのハニング窓の特性からピークを算出する方法があります。
A37, サンプル数 = 4096(2^12),分解能 = 10.767[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 220.003 : 0.022: 0.022 : .... 2: A(49) : 440.008 : 0.033: 0.033 : 0.002 3: E(56) : 660.009 : 1.977: 0.022 : -0.000 4: A(61) : 880.014 : 0.027: 0.027 : 0.000 5: Cis(65) : 1100.014 : -13.664: 0.022 : -0.000 6: E(68) : 1320.019 : 1.980: 0.025 : 0.000 7: G(71) : 1540.020 : -31.152: 0.022 : -0.000 8: A(73) : 1760.020 : 0.020: 0.020 : -0.000 9: H(75) : 1980.026 : 3.932: 0.022 : -0.000 10: Cis(77) : 2200.026 : -13.666: 0.020 : -0.000 ------------------------------------------------
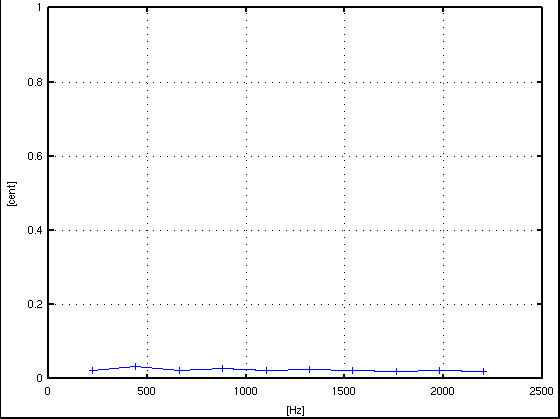
サンプル数 = 8192(2^13),分解能 = 5.383[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 220.003 : 0.026: 0.026 : .... 2: A(49) : 440.006 : 0.023: 0.023 : 0.001 3: E(56) : 660.009 : 1.977: 0.022 : 0.000 4: A(61) : 880.010 : 0.020: 0.020 : -0.000 5: Cis(65) : 1100.013 : -13.666: 0.020 : -0.000 6: E(68) : 1320.015 : 1.975: 0.020 : -0.000 7: G(71) : 1540.018 : -31.154: 0.020 : -0.000 8: A(73) : 1760.021 : 0.020: 0.020 : -0.000 9: H(75) : 1980.023 : 3.930: 0.020 : -0.000 10: Cis(77) : 2200.026 : -13.666: 0.020 : -0.000 ------------------------------------------------
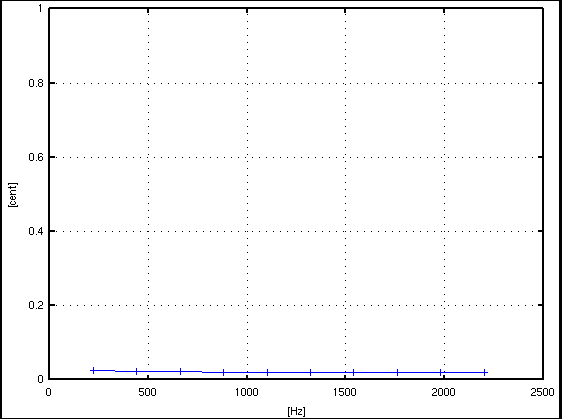
サンプル数 = 16384(2^14),分解能 = 2.692[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 220.003 : 0.022: 0.022 : .... 2: A(49) : 440.005 : 0.020: 0.020 : -0.000 3: E(56) : 660.008 : 1.975: 0.020 : -0.000 4: A(61) : 880.010 : 0.020: 0.020 : -0.000 5: Cis(65) : 1100.013 : -13.666: 0.020 : 0.000 6: E(68) : 1320.015 : 1.975: 0.020 : -0.000 7: G(71) : 1540.018 : -31.154: 0.020 : -0.000 8: A(73) : 1760.020 : 0.020: 0.020 : -0.000 9: H(75) : 1980.023 : 3.930: 0.020 : -0.000 10: Cis(77) : 2200.025 : -13.667: 0.020 : -0.000 ------------------------------------------------
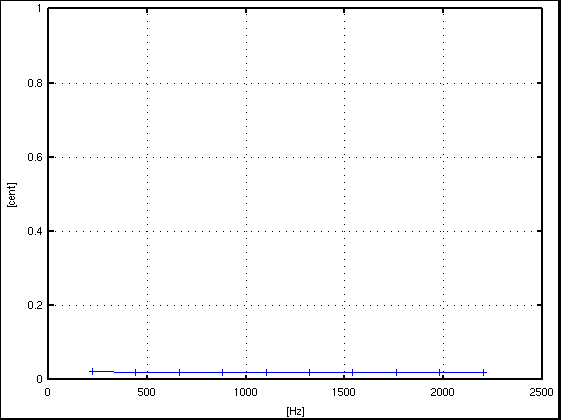
では インハーモニシティのある10倍音の場合です。 A37のWave信号は以下の様になります。
倍数 : Key# : 周波数[Hz] : 差[cent] : Inharmo. ---------------------------------------------- 1 : A(37) : 219.7553 : -1.9270 : -1.9270 2 : A(49) : 439.6843 : -1.2425 : -1.2425 3 : E(56) : 659.9612 : 1.8533 : -0.1017 4 : A(61) : 880.7605 : 1.4955 : 1.4955 5 : Cis(65) : 1102.2572 : -10.1374 : 3.5489 6 : E(68) : 1324.6276 : 8.0137 : 6.0587 7 : G(71) : 1548.0489 : -22.1493 : 9.0248 8 : A(73) : 1772.6996 : 12.4472 : 12.4472 9 : H(75) : 1998.7602 : 20.2360 : 16.3260 10 : Cis(77) : 2226.4127 : 6.9748 : 20.6611 ---------------------------------------------
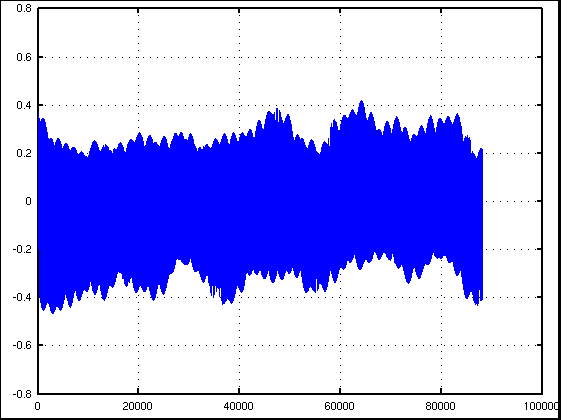
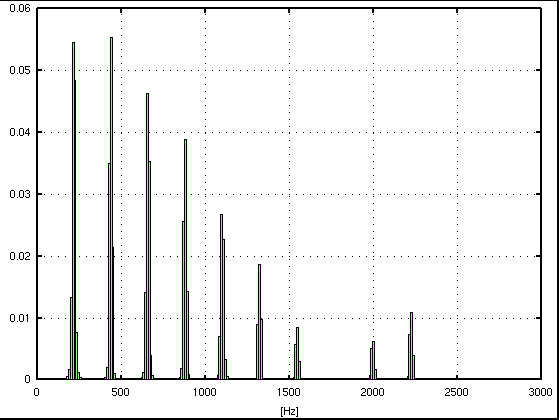
1. FFTのみでの測定です。 サンプル数 = 4096(2^12),分解能 = 10.767[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 215.332 : -37.129: -37.129 : .... 2: A(49) : 441.431 : 5.620: 5.620 : 3.021 3: E(56) : 656.763 : -6.558: -8.513 : -0.228 4: A(61) : 882.861 : 5.620: 5.620 : 0.755 5: Cis(65) : 1098.193 : -16.532: -2.846 : 0.145 6: E(68) : 1324.292 : 7.575: 5.620 : 0.336 7: G(71) : 1550.391 : -19.532: 11.642 : 0.369 9: H(75) : 2002.588 : 23.548: 19.638 : 0.322 10: Cis(77) : 2228.687 : 8.742: 22.428 : 0.289 --------------------------------------------------
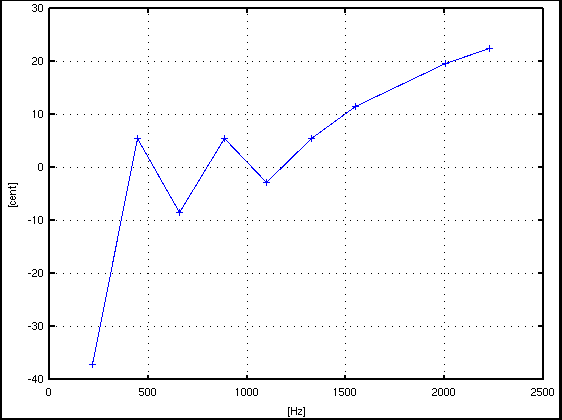
サンプル数 = 8192 (2^13),分解能 = 5.383[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 220.715 : 5.620: 5.620 : .... 2: A(49) : 441.431 : 5.620: 5.620 : -0.002 3: E(56) : 662.146 : 7.575: 5.620 : -0.001 4: A(61) : 882.861 : 5.620: 5.620 : -0.001 5: Cis(65) : 1103.577 : -8.066: 5.620 : -0.000 6: E(68) : 1324.292 : 7.575: 5.620 : -0.000 7: G(71) : 1550.391 : -19.532: 11.642 : 0.123 9: H(75) : 1997.205 : 18.888: 14.978 : 0.115 10: Cis(77) : 2228.687 : 8.742: 22.428 : 0.168 -------------------------------------------------
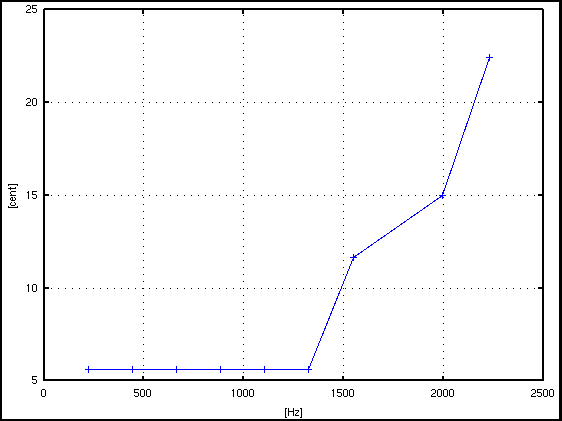
サンプル数 = 16384(2^14),分解能 = 2.692[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 220.715 : 5.620: 5.620 : .... 2: A(49) : 438.739 : -4.969: -4.969 : -0.598 3: E(56) : 659.454 : 0.523: -1.432 : 0.127 4: A(61) : 880.170 : 0.334: 0.334 : 0.182 5: Cis(65) : 1103.577 : -8.066: 5.620 : 0.328 6: E(68) : 1324.292 : 7.575: 5.620 : 0.228 7: G(71) : 1547.699 : -22.541: 8.633 : 0.229 9: H(75) : 1999.896 : 21.220: 17.310 : 0.245 10: Cis(77) : 2225.995 : 6.650: 20.336 : 0.229 -------------------------------------------------
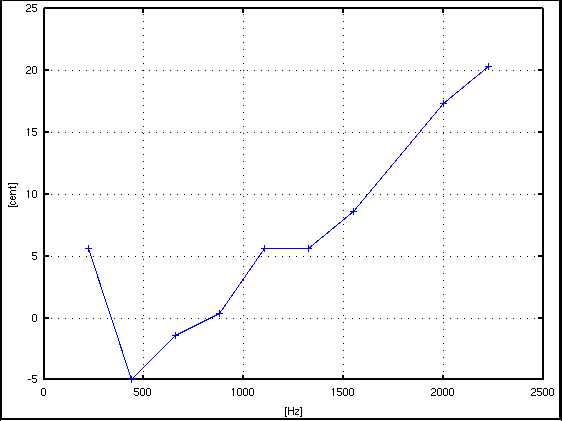
2. ピークピッキング法です。 A37, サンプル数 = 4096(2^12),分解能 = 10.767[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 217.509 : -19.716: -19.716 : .... 2: A(49) : 441.259 : 4.945: 4.945 : 2.147 3: E(56) : 657.553 : -4.475: -6.430 : -0.310 4: A(61) : 882.583 : 5.075: 5.075 : 0.545 5: Cis(65) : 1099.768 : -14.052: -0.366 : 0.131 6: E(68) : 1324.299 : 7.585: 5.630 : 0.258 7: G(71) : 1550.029 : -19.936: 11.238 : 0.304 9: H(75) : 2001.236 : 22.379: 18.469 : 0.273 10: Cis(77) : 2228.403 : 8.522: 22.208 : 0.258 --------------------------------------------------
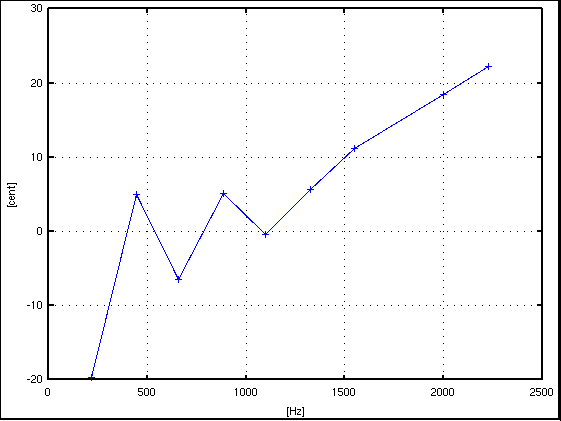
サンプル数 = 8192(2^13),分解能 = 5.383[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 220.606 : 4.761: 4.761 : .... 2: A(49) : 440.950 : 3.735: 3.735 : 0.325 3: E(56) : 661.063 : 4.741: 2.786 : 0.039 4: A(61) : 882.033 : 3.995: 3.995 : 0.098 5: Cis(65) : 1103.344 : -8.432: 5.255 : 0.113 6: E(68) : 1324.304 : 7.591: 5.636 : 0.089 7: G(71) : 1549.124 : -20.948: 10.227 : 0.159 9: H(75) : 1997.565 : 19.201: 15.291 : 0.159 10: Cis(77) : 2227.608 : 7.904: 21.590 : 0.192 ------------------------------------------------
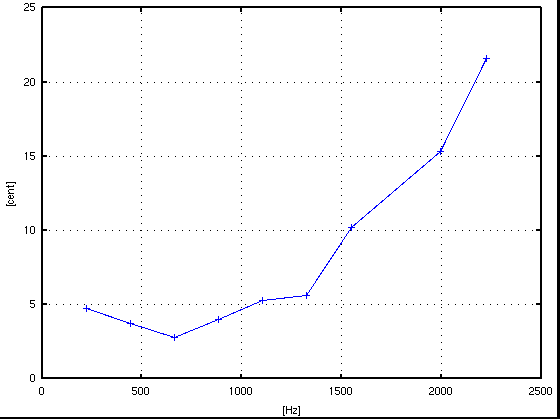
サンプル数 = 16384(2^14),分解能 = 2.692[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 220.382 : 3.007: 3.007 : .... 2: A(49) : 439.059 : -3.708: -3.708 : -0.195 3: E(56) : 659.514 : 0.679: -1.276 : 0.183 4: A(61) : 880.266 : 0.523: 0.523 : 0.216 5: Cis(65) : 1102.430 : -9.866: 3.820 : 0.270 6: E(68) : 1324.318 : 7.610: 5.655 : 0.238 7: G(71) : 1547.736 : -22.500: 8.674 : 0.237 9: H(75) : 1999.352 : 20.748: 16.838 : 0.244 10: Cis(77) : 2226.045 : 6.688: 20.375 : 0.233 -------------------------------------------------
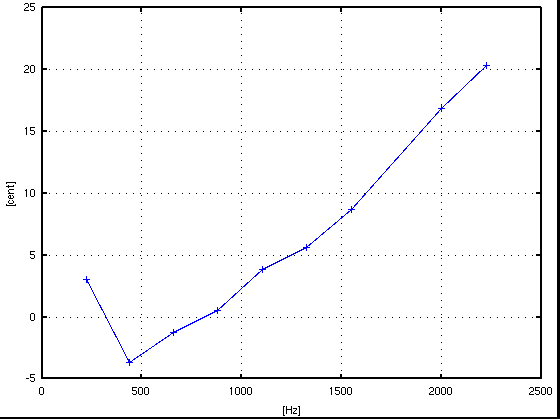
3. 補間公式です。
A37, サンプル数 = 4096(2^12),分解能 = 10.767[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 219.758 : -1.904: -1.904 : .... 2: A(49) : 439.693 : -1.210: -1.210 : 0.247 3: E(56) : 659.970 : 1.876: -0.079 : 0.235 4: A(61) : 880.774 : 1.522: 1.522 : 0.232 5: Cis(65) : 1102.270 : -10.117: 3.570 : 0.231 6: E(68) : 1324.645 : 8.037: 6.082 : 0.230 7: G(71) : 1548.070 : -22.126: 9.048 : 0.229 9: H(75) : 1998.787 : 20.259: 16.349 : 0.229 10: Cis(77) : 2226.442 : 6.997: 20.684 : 0.229 ------------------------------------------------
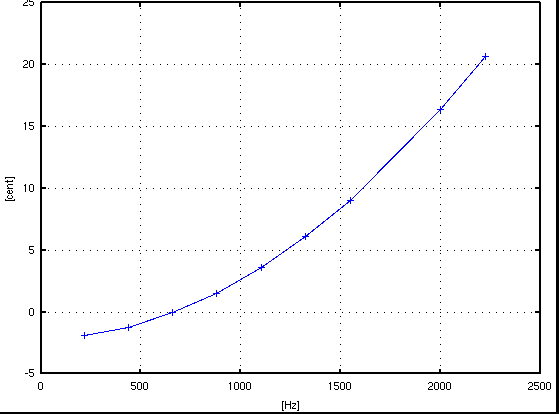
サンプル数 = 8192(2^13),分解能 = 5.383[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 219.759 : -1.901: -1.901 : .... 2: A(49) : 439.690 : -1.219: -1.219 : 0.245 3: E(56) : 659.970 : 1.876: -0.079 : 0.235 4: A(61) : 880.772 : 1.517: 1.517 : 0.232 5: Cis(65) : 1102.271 : -10.116: 3.570 : 0.231 6: E(68) : 1324.643 : 8.034: 6.079 : 0.230 7: G(71) : 1548.068 : -22.128: 9.046 : 0.229 9: H(75) : 1998.783 : 20.256: 16.346 : 0.229 10: Cis(77) : 2226.439 : 6.995: 20.682 : 0.229 ------------------------------------------------
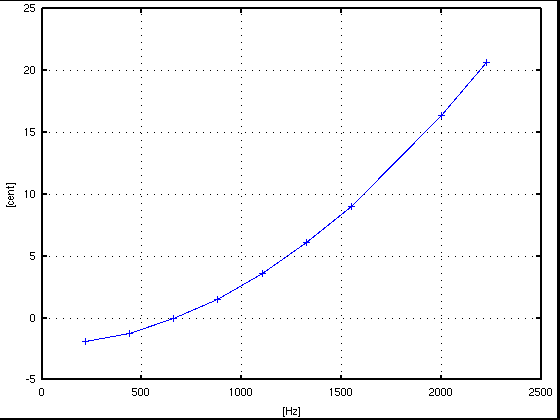
サンプル数 = 16384(2^14),分解能 = 2.692[Hz]
倍数: Key# : 周波数[Hz] : c.equal: c.pure: I.const. --------------------------------------------------- 1: A(37) : 219.758 : -1.905: -1.905 : .... 2: A(49) : 439.689 : -1.223: -1.223 : 0.244 3: E(56) : 659.969 : 1.873: -0.082 : 0.235 4: A(61) : 880.771 : 1.515: 1.515 : 0.232 5: Cis(65) : 1102.270 : -10.117: 3.569 : 0.231 6: E(68) : 1324.643 : 8.033: 6.078 : 0.230 7: G(71) : 1548.067 : -22.130: 9.045 : 0.229 9: H(75) : 1998.783 : 20.256: 16.346 : 0.229 10: Cis(77) : 2226.438 : 6.994: 20.681 : 0.229 ------------------------------------------------
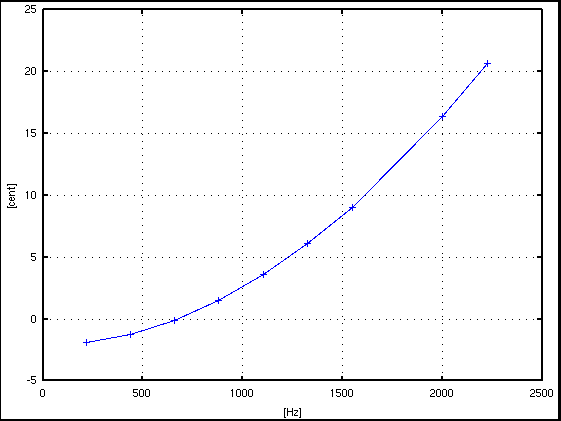
以上の結果などを踏まえて Java Pitch (JP)や インハーモニシティを求めて (In pursuit of inharmonicity)には 3.の補間公式を使用しています。
(※改訂履歴:
v0.1.2['14/02/14] HTML5を別のページに分離しました。
v0.1.1['14/02/11]
[Text]テキスト表示を修正して変更しました。
v0.1['13/11/16])

HTML5版です。