「時間窓巾調整によるピッチ周波数の精密計算法」(著:高澤 嘉光) と云う論文があります。
しかし
今回は久しぶりに長い時間かかってしまいましたが
今だに再現出来ていません。
そうしてジタバタしてる間に
そこからのアイデアを使って
そこそこ動作する別のものが出来てしまいましたので
使ってみて下さい。
例えば 430[Hz]とその4倍音までのWave信号があります。
それをJP(Java Pitch)で見てみます。サンプル数は 512(2の9乗)個です。
さらに 256(2の8乗)個...
128(2の7乗)個...
64(2の6乗)個(高さを変えています)...
そして 32(2の5乗)個としてみます。
ピークが識別出来ていません。 ここの「DFT」ではスペクトルの幅を見やすい様に狭くしています。
メインローブが重なってしまっています。 ハニング窓の式からピーク値の1/2をピークの両側に加えれば メインローブの重なりがなくなります。 (以下はハニング窓の周波数特性です。)
また フーリエ変換の性質として
観測間隔を周期に合わせるとサイドローブの遺漏が無くなります。
(左は丁度のサイズの場合、右は少しずれている場合です。)
そこで DFT(離散フーリエ変換(discrete fourier transform))を使って サンプル数を変化させる事でスペクトルの遺漏が一番小さくなる所が "基音"と判断されます。
インハーモニシティ有りでも 例えば「Jwv」の a110.wavですが
上右の様に測定出来ます。しかし 単信号は正確ではありませんし 測定位置によって最大値も変わります。
(※ 変更履歴：
v0.1.2['19/04/14] HTML5版 DFTを追加しました。
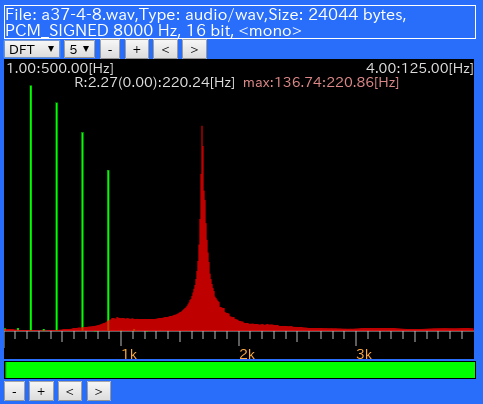
HTML5版です。
v0.1.1['16/02/13]
[Adjust]ボタンに [Stop]を追加したトグルボタンに変更しました。
マウスカーソルで Waveの範囲を選択出来る様にしました。
v0.1['16/02/01])
画面上 [ 5 ... 8 ] セレクタ: サンプル数を選びます。 2の乗数で表示していて 5=32, 6=64, 7=128, 8=256個ですが [Adjust]ボタンが動作するのは [5]のみです。
[ || ]スライダ: 手動で最適値を選ぶ時に使用します。
[ /1 ... /8 ] セレクタ: 最適値を4段階で切替えます。
---------------- /1 : 0.7 - 1.4 /2 : 1.4 - 2.8 /4 : 2.8 - 5.6 /8 : 5.6 - 11.2
そしてその測定範囲は(画面上端に表示されます) サンプリング周波数によって以下の様に変わります。
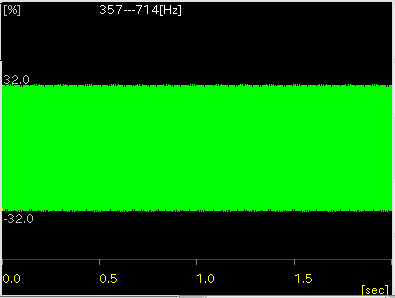
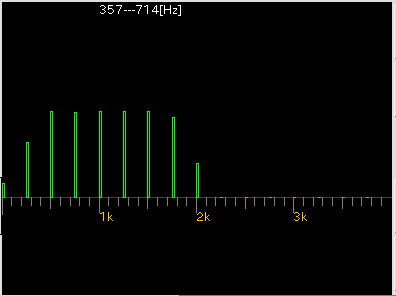
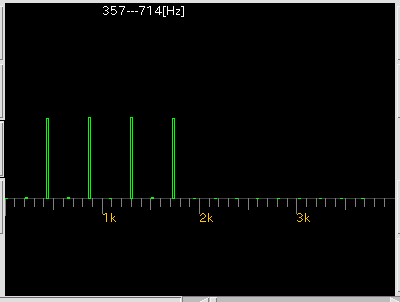
＼ 8000 : 11025 : 22050 : 44100 (サンプリング周波数 [Hz]) --------------------------------------------------------------------- /1 : 357-714 : 492-984 : 984-1969 : 1969-3938 (測定範囲 [Hz]) /2 : 179-357 : 246-492 : 492-984 : 984-1969 /4 : 89-179 : 123-246 : 246-492 : 492-984 /8 : 45- 89 : 62-123 : 123-246 : 246-492
[ ] テキスト入力: 最適値を直接入力する時に使用します。
[test430.wav]は[Adjust]の結果 1.16で(max:53.31408)
431.03448[Hz]ですが
テキスト入力で追い込む事で 1.161795(max:58.70556)
430.36853[Hz]まで求まります。
しかし論文では 調整率 1.16279で 430.000258[Hz]となっていますので
まだまだです；
[ Adjust ] トグルボタン: スライダの範囲を自動的に測定して 最大となる最適値(周波数)を表示します。 動作中に停止する場合にもクリックして下さい。
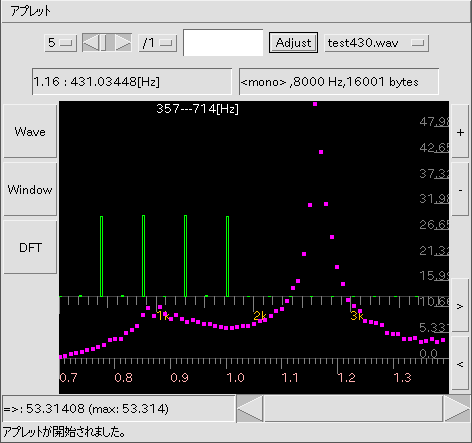
[ test430.wave ] セレクタ: Waveファイルを選びます。
[ ] テキスト表示: 最適値とその周波数を表示します。
[ ] テキスト表示: Waveファイルのデータを表示します。
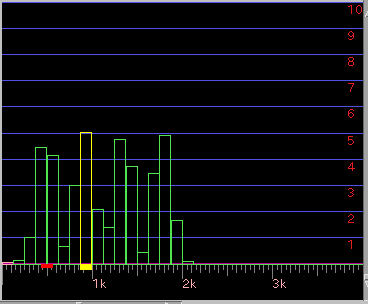
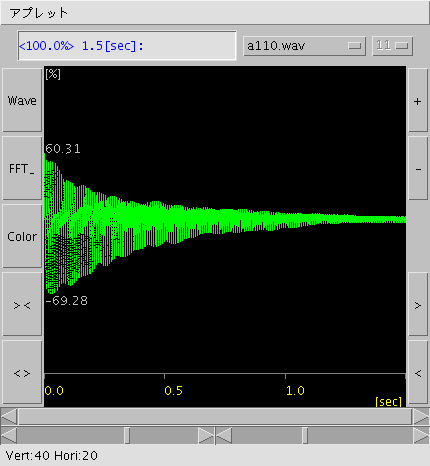
(※)画面左 [ Wave ] ボタン: Wave信号を表示します。
(※)ドラッグでマウスカーソルが現れます。
測定範囲以上になればカーソルがマゼンタ色から白色に変わります。
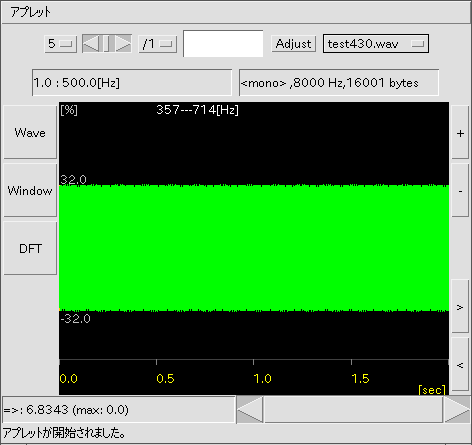
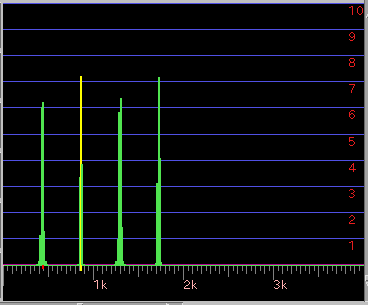
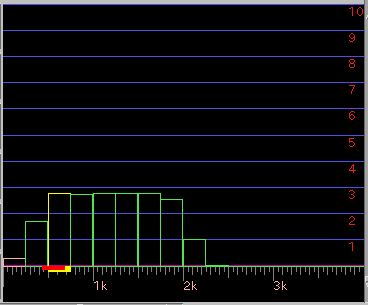
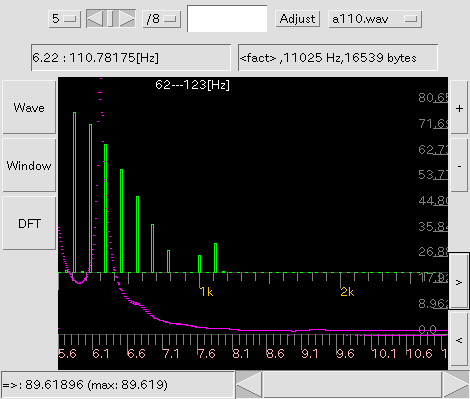
[ Window ] ボタン: 窓関数を通ったWave信号を表示します。 (グラフは[7]の場合です。)
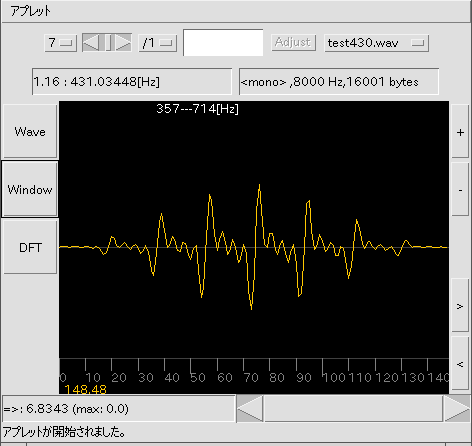
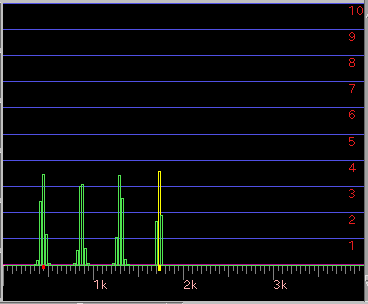
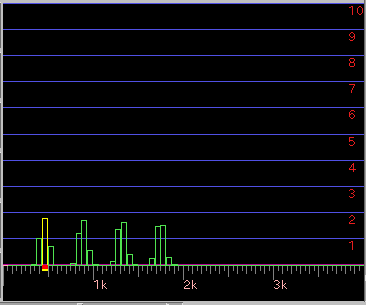
[ DFT ] ボタン: 最適値を計算したスペクトルを表示します。 [5]以外では 普通にスペクトルを表示します。
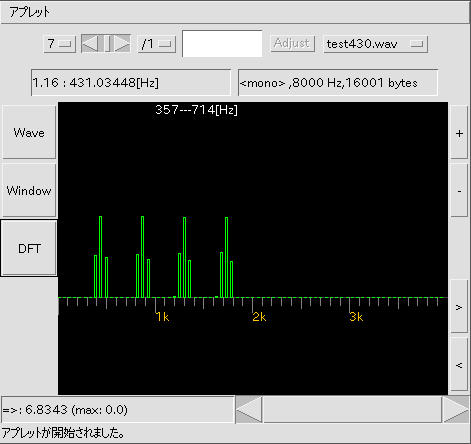
画面右 [ + | - ] ボタン: 画面の上下を増減します。
[ > | < ] ボタン: [Wave][DFT]の左右を増減します。
画面下 [ ] テキスト表示: [5]スペクトルの最適値と [Adjust]動作後の最大値を表示します。
[ || ]スライダ: Wave信号の表示範囲を表します。
まるでトイカメラかトイピアノの様かも知れません。
しかし
これまでのサンプル数を増やして分解能を高めるのとは逆に
32個のサンプル数+ハニング窓のアイデアは
ユニークでシンプルで斬新です。