ピッチ抽出の試み(その1)(Pitch) v0.6
周波数の測定方法として
周期測定・周波数カウンター・ヘテロダイン法・パワー
スペクトル法などがありますが
その中に線形予測法(Linear Prediction)
によるスペクトル分析法があります。
その中からさらに PARCOR方式
(Partial
Autocorrelation)
<偏自己相関>の係数を計算機で求める方法として
Durbin法というものがありす。
《 FORTRAN プログラム 》
それらのプログラムは(見やすくするため
continueを追加してデータの入力部分は省略しています)
% wc *.f
36 58 874 durb.f
39 65 828 fdpk.f
48 70 1042 fft.f
41 66 816 formt.f
164 259 3560 total
全て合わせても164行ですので「f2c」というプログラムで
C言語に変換してから Java言語に再構成して見ました。
(因みに formt.java は (v0.6)713行ほどあります)
FORTRANプログラムでは 10[KHz]でサンプリングされた
256個の音声サンプルから Durbin法で 15個の線形予測係数を求め
それに対して 256個の FFT処理によって周波数間隔
10[KHz] / 256 = 39.06[Hz]毎のスペクトル値を求め
そのうちの半分(128個)のスペクトル値から
ピークピッキング法により
ホルマント周波数・帯域幅・ピーク値を求めています。
その周波数間隔の式から
- 44100[Hz] / 256 = 172.266[Hz] ( L = 8 )
- 44100[Hz] / 512 = 86.133[Hz] ( L = 9 )
- 44100[Hz] / 1024 = 43.066[Hz] ( L = 10 )
- 8000[Hz] / 256 = 31.25[Hz]
- 8000[Hz] / 512 = 15.625[Hz]
- 8000[Hz] / 1024 = 7.8125[Hz]
サンプリング周波数を小さくして
サンプル数を多くすれば周波数分解能が上がると思われます。
A(49) 440[Hz] を makewavex で作成した
インハーモニシティあり・4倍音・サンプリング周波数
44100[Hz]の場合です。
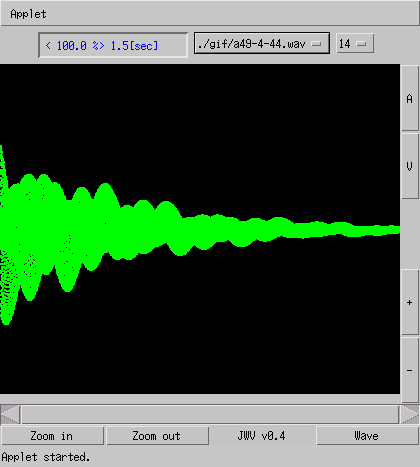
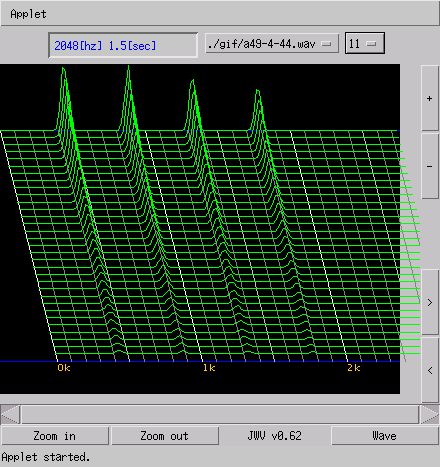
上はそのWave波形図とFFT図です。
 (133KB)
(133KB)
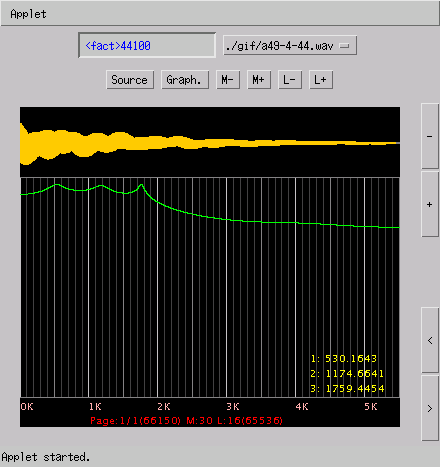
しかし 4つに分解されません。
「sox」で サンプリング周波数を 44100[Hz]から
8000[Hz]に変更して見ます。
% sox -t wav -r 44100 a49-4-44.wav -r 8000 a49-4-8.wav
 (24KB)
(24KB)
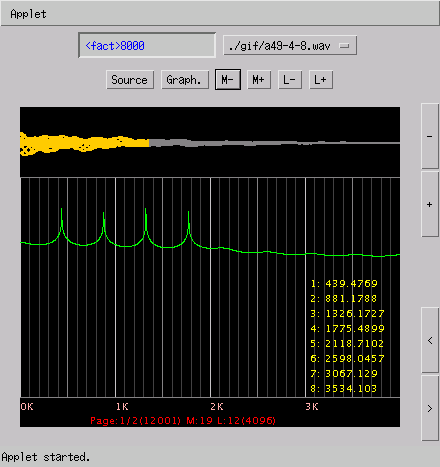
〔構成周波数〕
1 : 440.0000
2 : 881.5262
3 : 1326.1138
4 : 1775.3155
周波数は上記のはずですが 画面の出力結果は…
A(37) 219.516[Hz]の4倍音の場合です。
 (24KB)
(24KB)
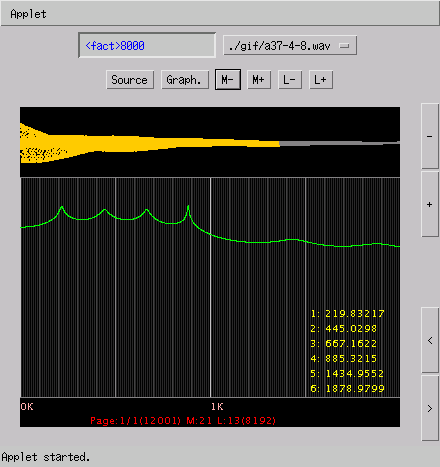
〔構成周波数〕
1 : 219.5160
2 : 439.4125
3 : 660.0713
4 : 881.8761
さらに A(25) 109.5125[Hz]の4倍音の場合です。
 (24KB)
(24KB)
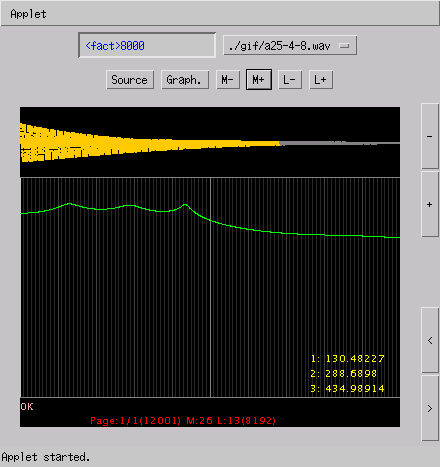
〔構成周波数〕
1 : 109.5125
2 : 219.1200
3 : 328.9174
4 : 439.0000
「RCT」のように A(1)27.5[Hz]で
1セントまでの正確さとは行かないようです。
使い方:
(※ 変更履歴:
v0.6['13/03/03] 画面構成を変更しました。
cssファイルを別にしました。
v0.5.2['12/11/11]
ReadWave.javaのmonoとStereoの切替えの不具合を訂正しました。
v0.5.1['07/11/29] ReadWave.java(v0.2)に修正しました。
v0.5['05/9/4] FFTを変更しました。
Wave信号の読み込みを別(クラス)にしました。
v0.4['04/2/21]
S・M・LでJava画面のサイズを変更出来るようになりました。
v0.3 ボタン位置の変更・信号波形の表示)
画面上 [ <fact> 8000[Hz]: 1.5[sec] ]テキスト画面:
Waveファイルのタイプとサンプリング周波数[Hz]:時間[sec]
を表示します。
- [ a49-4-8.wav ]:サンプルのWave波形を選びます。
- a49-4-8.wav:
(24KB) A(49) 440[Hz] 4倍音まで Sampling 8000[Hz]
- a49-4-44.wav:
(133KB) A(49) 440[Hz] 4倍音まで Sampling 44100[Hz]
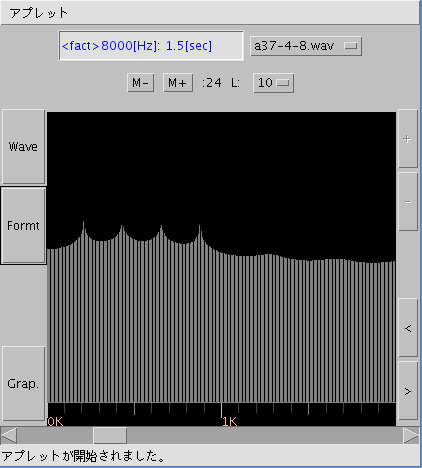
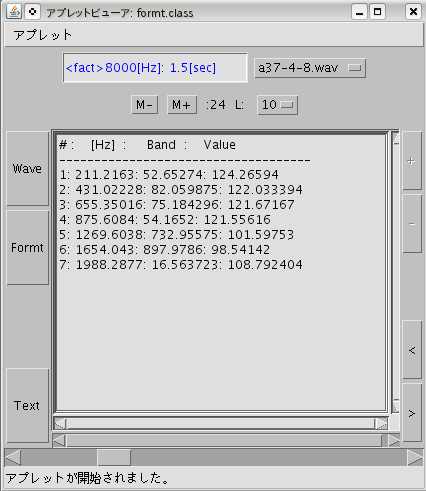
- a37-4-8.wav:
(24KB) A(37) 219.516[Hz] 4倍音まで Sampling 8000[Hz]
- a25-4-8.wav:
(24KB) A(25) 109.513[Hz] 4倍音まで Sampling 8000[Hz]
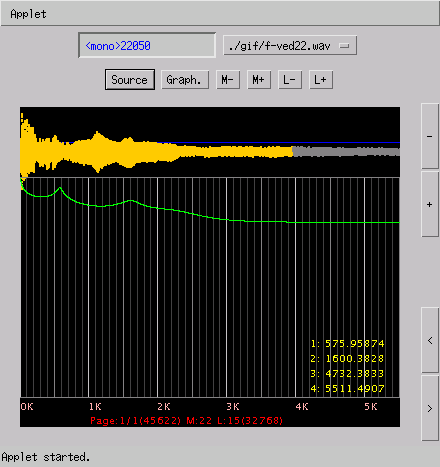
- f-ved22.wav:
(92KB) ピアノ音 Sampling 22050[Hz]
- f-ved8.wav:
(34KB) ピアノ音 Sampling 8000[Hz]
「 Source 」
トグルボタンで 画面上部の信号波形の表示/非表示
を切り替えます。削除しました。
「 L / B 」トグルボタン:
[Formt]画面の表示を
線グラフ(Line)か棒グラフ(Bar)に切替えます。
削除して[Formt]トグルボタンに移動しました。
「 M- 」「 M+ 」ボタン:
Durbin法の変数 M(線形予測係数)を増減します。
「L- | L+」:
Durbin法の変数 L(サンプル数)を変えます。
削除してセレクタに変更しました。
(※)「 L: 1 ... 8 ... 」セレクタ:
変数 L(サンプル数)を選択します。
(最大値はWaveファイルのサイズによって変動します。)
(※)画面左 「 Wave 」ボタン:
wave波形を表示します。
下段のスライダでサンプル位置が移動します。
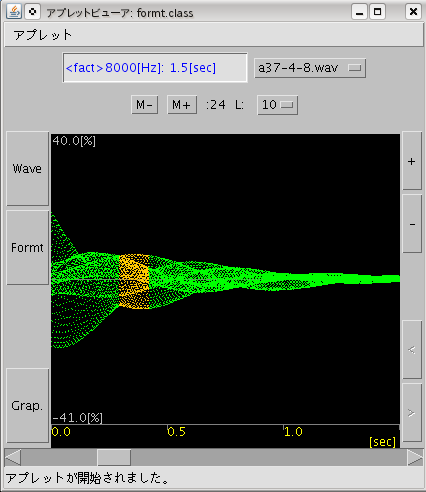
(※)「 Formt 」ボタン:
Durbin法の測定結果を表示します。
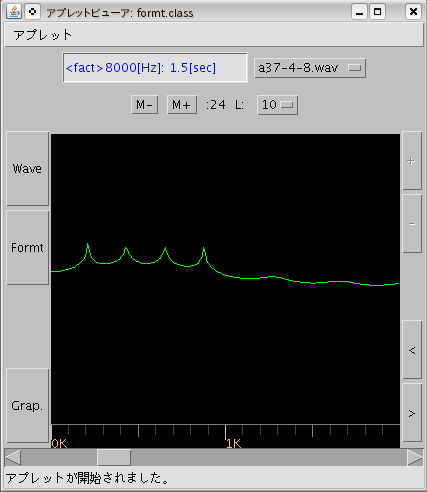
[Formt]ボタン2度のクリックで線グラフ表示と
棒グラフ表示が切り替わります。
「 Grap. / Text 」トグルボタン:
画像とテキスト画面を切り替えます。
「Text」では[#:ピーク周波数 / 帯域幅 / ピーク値]
を表示します。
画面右側 「 - 」「 + 」ボタン:
(Page):経過時間毎に表します。
変わりに下段のスライダーに変更しました。
[Wave]画面で信号の高さを増減します。
「 < 」「 > 」ボタン:
[Formt]画面の横スケールを拡大・縮小します。
画面下段 スライダ:
wave信号のサイズとサンプル幅を表しています。
[Wave]画面では
現在測定している部分をオレンジ色
で示しています。
画面下部には
[Page:現在のページ番号 / 総ページ数(データ数)
M:Mの値 L:Lの値(サンプル数)]が
赤色で表示されています。
削除しました。
- 画面右下には
黄色で
「ピーク順番:ピーク周波数」を表示しています。
削除しました。
変わりに[Text]画面で参照します。
では ピアノの音はどうでしょう?
参考にするピアノ音はJava Wave Viewer
(Java Wave Viewer)で 「Fille」として取り上げた単音を
サンプリング周波数を変えて見てみます。
- 22050[Hz]
 (92KB)
(92KB)
- 8000[Hz]
 (34KB)
(34KB)
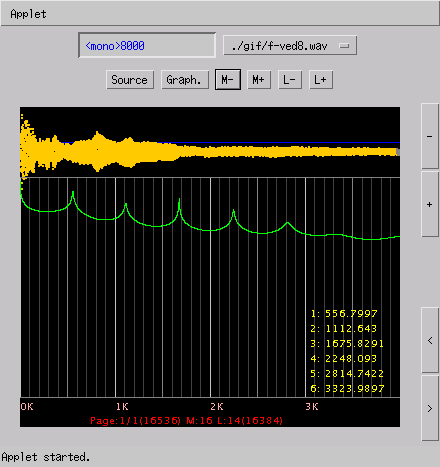
8000[Hz]では以下のようなピーク値が現れています。
1: 556.7997 / 53.488686 / 142.25995
2: 1112.643 / 84.83396 / 134.22902
3: 1675.8291 / 17.415987 / 137.66922
4: 2248.093 / 55.755123 / 130.02992
5: 2814.7422 / 287.4275 / 121.181725
6: 3323.9897 / 1530.1614 / 112.94095
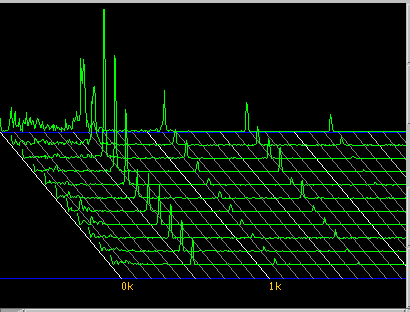
そのFFTの波形のゲインを上げて見ると ノイズの中に
6倍音ぐらいまであるように見受けられます。
因みに サンダーソン氏の式のインハーモニシティでは
ピッチ441[Hz]でキー C#(53)は以下の値です。
〔構成周波数〕
1 : 556.129
2 : 1114.69
3 : 1678.13
4 : 2248.93
5 : 2829.64
6 : 3422.86
分解能を上げるために「sox」でサンプリング周波数を小さくして見ます。
(音声は正常には聞こえません)
% sox -r 8000 a25-4-8.wav -r 4000 a25-4-4.wav
 (12KB)
(12KB)
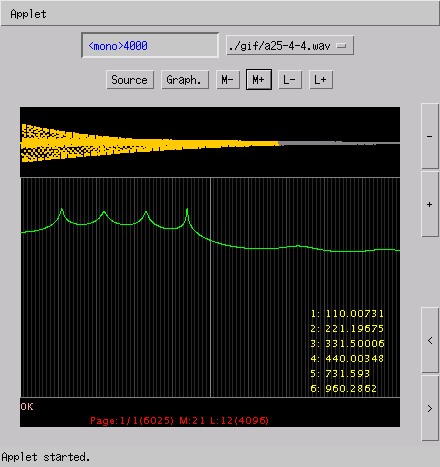
〔構成周波数〕
1 : 109.5125
2 : 219.1200
3 : 328.9174
4 : 439.0000
% sox -r 8000 a25-4-8.wav -r 2000 a25-4-2.wav
 (6.2KB)
(6.2KB)
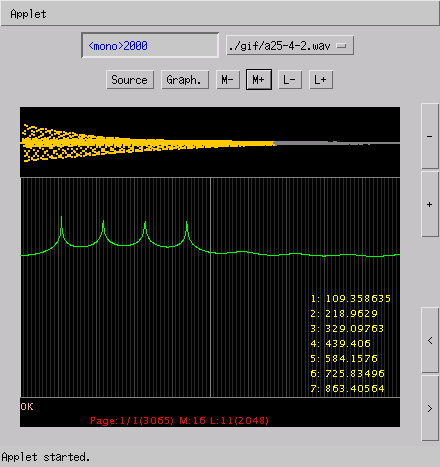
% sox -r 8000 a13-4-8.wav -r 2000 a13-4-2.wav
 (6.2KB)
(6.2KB)
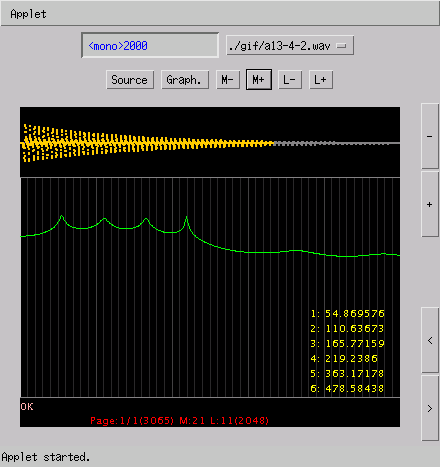
〔構成周波数〕
1 : 54.5707
2 : 109.1650
3 : 163.8067
4 : 218.5193
% sox -r 8000 a13-4-8.wav -r 1000 a13-4-1.wav
 (3.3KB)
(3.3KB)
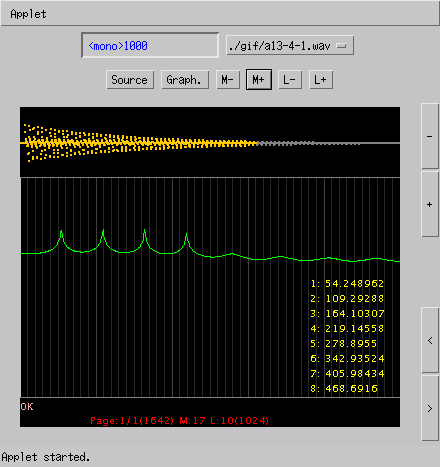
% sox -r 8000 a1-4-8.wav -r 500 a1-4-05.wav
 (2.2KB)
(2.2KB)
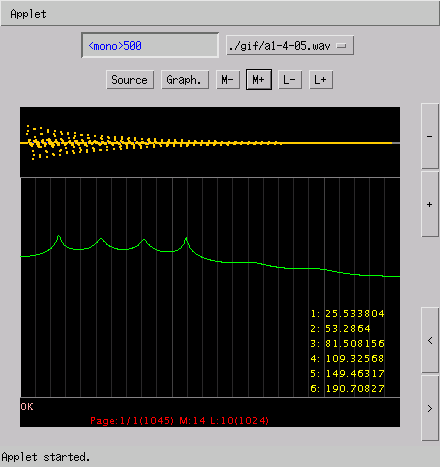
〔構成周波数〕
1 : 27.1154
2 : 54.2367
3 : 81.3697
4 : 108.5204
% sox -r 8000 a1-10-8.wav -r 1000 a1-10-1.wav
 (3.3KB)
(3.3KB)
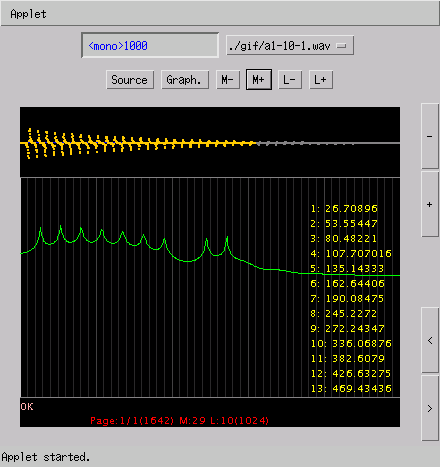
〔構成周波数:ボリューム〕
1 : 27.1154 : 0.244
2 : 54.2367 : 0.225
3 : 81.3697 : 0.196
4 : 108.5204 : 0.159
5 : 135.6946 : 0.118
6 : 162.8981 : 0.075
7 : 190.1371 : 0.035
8 : 217.4172 : 0.000
9 : 244.7445 : 0.027
10 : 272.1249 : 0.045
- a25-4-4.wav:(12KB) A(25) 109.5125[Hz]
4倍音まで Sampling 4000[Hz]
- a25-4-2.wav:(6.2KB) A(25) 109.5125[Hz]
4倍音まで Sampling 2000[Hz]
- a13-4-2.wav:(6.2KB) A(13) 54.5707[Hz]
4倍音まで Sampling 2000[Hz]
- a13-4-1.wav:(3.3KB) A(13) 54.5707[Hz]
4倍音まで Sampling 1000[Hz]
- a1-4-05.wav:(2.2KB) A(1) 27.1154[Hz]
4倍音まで Sampling 500[Hz]
- a1-10-1.wav:(3.3KB) A(1) 27.1154[Hz]
10倍音まで Sampling 1000[Hz]
これまでのWave信号をFormtなどで見てみます。
View Wave Files
参考文献:
- コンピュータ音声処理 安居院 猛/中嶋 正之 産報出版 1980
- 音の科学 井口 征士(他) 朝倉書店 1989
Dobashi.M
Last modified: 1月 03日 火 14:08:25 2023 JST


















