“振動”の説明によると 抵抗のない床の上に質量 Mがあり
それが壁にバネとダンパで継っています。
質量 Mが移動する時 バネはその変移量に比例した抵抗力を出します。
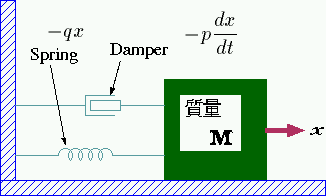
そこで ダンパの係数を p・バネの強さを示す係数を qとすると 質量 Mに加わる力 Fは...
となり それをニュートンの運動方程式...
に入れると...
各種の運動を示す典型的な方程式となります。
その解法はここでの説明ではありませんが
それを「ルンゲ・クッタ法」で解いたプログラムがありましたので
それをJavaに移植して見ました。
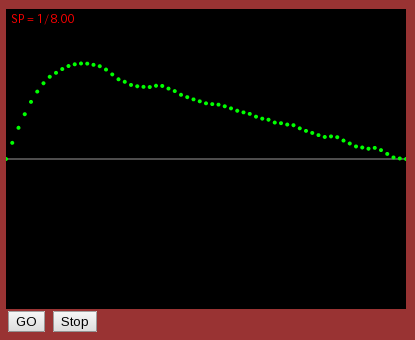
（横軸は時間 t・縦軸が変位 xです）
バネの強さQとダンパの強さPをスライドバーで可変するようにしてあります。
3.の時の振動数は固有振動数で この系特有の振動数だそうです。
1.のグラフは何処かで見た事がないでしょうか？
「実験室」でピアノの音を再現した時のグラフに似たようなのがありました。
ピアノの方はもっと周波数が高いのでラッパの先 朝顔型をしていましたが
同じ減衰振動です。
次は 上の式に外から力がかかった場合です。
外部の力としては 正弦波(W)で その振幅は固定としています。
1. P = 1, Q = 4の場合
時間が経つと外力と同じ振動数で振動させられています。
しかし振幅は固有振動数(W = 2) の時に最大で
それより大きくても小さくても振幅は小さくなります。
これを共振現象と言います。
ピアノで言えば 弦1本だけで鳴っているのではなく 様々な倍音の弦から駒・ 響板・さらに鉄骨・外装・置かれた環境などまでにも継って行きます。
様々な波の性質を表す“波動方程式”と言うものがあります。
弦の振動が 振幅 y・時間 t・位置 xによってどう表されるかを
示す方程式です。
この場合は 弦の両端は固定され,
弦は分割した緑の点で表しています。
基音の場合は弦の中央が一番大きく振動します。
（振幅は拡大して表現しています。また初期値をサイン波としています）
振幅の大きさは時間とともに変わり その振動数が音の周波数となります。
参考までにスライドバーで周波数を少し変えられるようにしてあります。
その方程式の解法は説明出来ませんが
「ガウス・ザイデル法」のプログラムを同じくJavaに移植して見ました。
同じ波動方程式を
「差分方程式」で解いたプログラムがありましたので
Javaに移植しました。
打弦点を変えて弦の動きの変化を見て下さい。
HTML5版です。
上記の“弦の振動”の時 弦はどのような音を発してるのでしょう？
音ではありませんが 弦の振動の計算式があります。
ハープの様に三角形に弦に自由振動を起こした時（撥弦）
また ピアノのようなインパルスの場合（打弦）
ではその倍音部分の大きさはどう決まるのでしょう?
（ピアノの場合打弦点は 1/8と経験的に決められているようですが）
(1)(2)の式で sin mπ(x0/l)の部分が打弦点
x0と次数 mの関係する所で
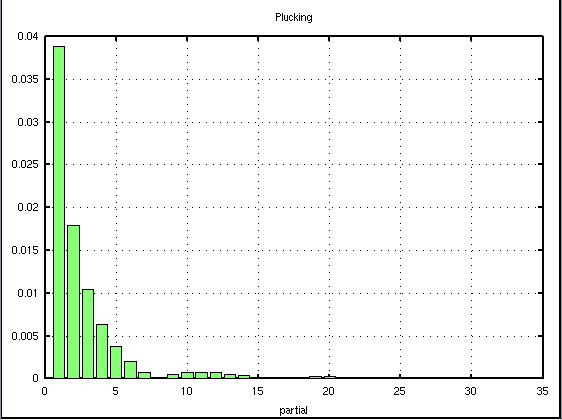
その関係式だけを取り出してグラフにして見ました。
（横軸が倍音次数 m・縦軸は相対的な大きさです）
ハープ弦を 撥弦位置で見てみます。
横軸が倍音数で緑色の縦の棒グラフが
その大きさです。
白色の線は その倍音を全て合わせた時の波形を表します。
倍音数(Partial)を 1にすると一つのサイン波のみになるのが判ります。
ピアノ弦を 打弦位置で見てみます。
(1)(2)の式に“時間関数”成分を加えました。
（ピアノの場合 インパルス（衝撃音）が元なのですが
その為には倍音数を∞（無限大）まで合成しなくてはなりません。
現在は40倍までですが それが400倍でも1000倍でも少し先端が尖ったぐらいで
動作はどんどん遅くなり実用になりませんので
とりあえず40倍としています）
先の波動方程式(1)から ピアノ弦の方程式が様々研究・ 実験されています。
Y = 変位 x = 弦の軸方向の位置座標 t = 時間 T = 張力 I = 2次モーメント E = 縦弾性係数 S = 断面積 ρ = 密度 σ = 弦の単位長さの質量 κ = ジャイレーション半径（？） r = 空気摩擦抵抗 b = 減衰係数 f() = ハンマーの方程式
今では 駒・響板・そしてハンマーまでも方程式で計算され,
整音作業までもシミュレーションされる時代になって来ましたし,
インハーモニシティについての理解も深まって来た様に思います。
願わくば パーソナルコンピューター上で誰でも自由に
そうした創造的な実験が出来るように成りますように…
2010年「クラヴィコードにおける弦振動の解析 -ヘルムホルツからの考察」高澤 嘉光 (音楽音響研究会資料 MA2010-5) が発表されました。
そこには これまでの弦振動の ギター・ハープなどの撥弦(plucking)、 ピアノなどの打弦(striking)、ヴァイオリンなどの擦弦(bowing)に加えて クラヴィコードを第4の振動方式として撞弦(pushing)と名付けています。
そしてそれらの振動を ヘルムホルツ波(Helmholtz motion)の観点から見ています。
始めに クラヴィコードの弦振動(撞弦 - pushing)を差分法で求めます。
(以下 HTML5版 4点)
>
(※v0.6: HTML5のcanvasとJavaScriptで表示します。)
(実際は 左端のタンジェントの移動距離は 5[mm]で 弦長は1000[mm]です)
[ Stop ]ボタン：弦の振動を停止します。
[ GO ]ボタン：弦の振動を再開します。
スライダー： クラヴィコードではタンジェントの移動時間の分割数を変えています。 それ以外は[打 | 撥 | 擦]弦位置を変更します。
([ Disp. ]トグルボタン：グラフの表示を弦振動 又はヘルムホルツ波(又は左右の合成波)に切替えます。)
([ + | - ]ボタン：画面上下幅を増減します。)
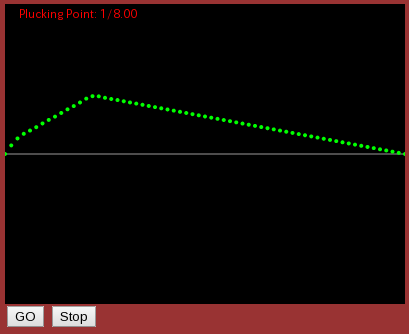
次は チェンバロの弦振動(撥弦 - plucking)です。
ダランベール(d'Alembert)形式では 「撥弦運動は弦に沿った正方向と負方向の2つの進行波の和で表される」 事を示しています。
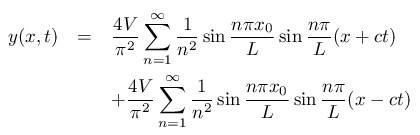
それを ヘルムホルツ波(Z波)で表します。
>
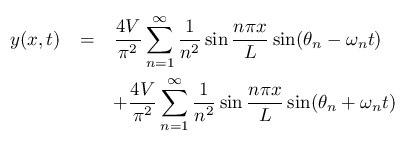
(※v0.6: HTML5のcanvasとJavaScriptで表示します。)
「撥弦によって 右回りと左回りの2つのヘルムホルツ波が発生する」 事を示しています。
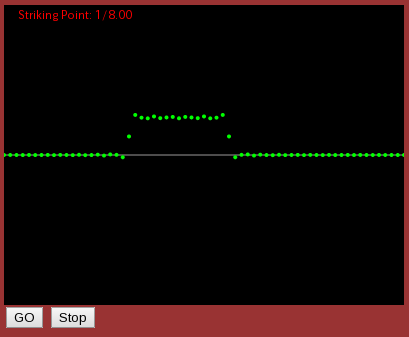
次は 打鍵振動(打弦 - striking)です。
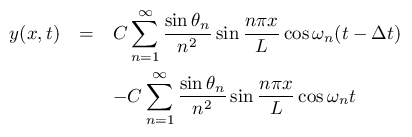
「打鍵振動は Δtの間隔で撥弦された1回目の振動と2回目の振動の差分である」 そうです。
それを ヘルムホルツ波(Z波)で表します。
>
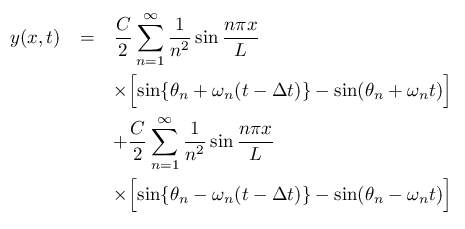
(※v0.6: HTML5のcanvasとJavaScriptで表示します。)
「打鍵振動は
右周りヘルムホルツ波と左回りヘルムホルツ波の時間差Δtの
差分の和である」事を表します。
そして 打鍵でヘルムホルツ波は右回りと左回りのそれぞれ 2個
計4個が現れます。
ピアノの加重時間 Δtはハンマーヘッドの軟硬度と密接に関係していて
Δtとモード成分の強さQnとの関係は以下の式で表されます。
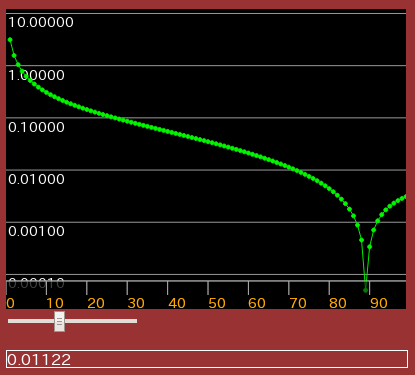
Δt/T(振動の周期)をパラメータにしたQnの絶対値を グラフにしてみます。(横軸は倍音数で縦軸はデシベルです)
加重時間Δtが短い程 高いモードが強くなっているのが分かります。 また Δtが長くなるとミッシング・モード(消失する倍音)が現れます。 [§]
そして ヴァイオリン(擦弦 - bowing)です。
>
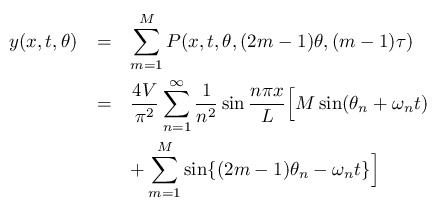
(※v0.6: HTML5のcanvasとJavaScriptで表示します。)
「復合Z波は
M個の右回りと左回りのヘルムホルツ波から構成されているが
右回りは位相が全て一致しているが
左回りは2θづつ遅れている」事を表しています。
(運弓によって擦弦位置が弦の10分の1で Mは約10になりますが
時には駒近くで Mが20に達する事もあるそうです)
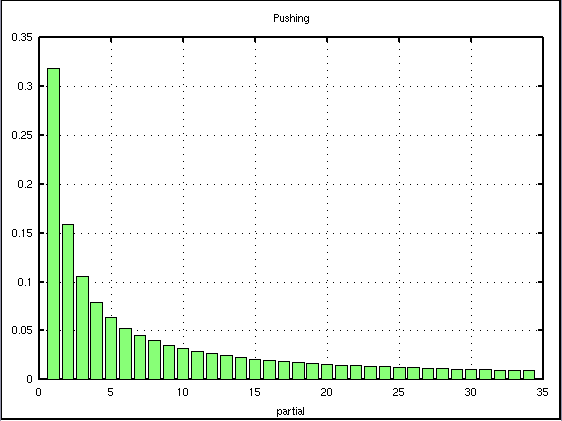
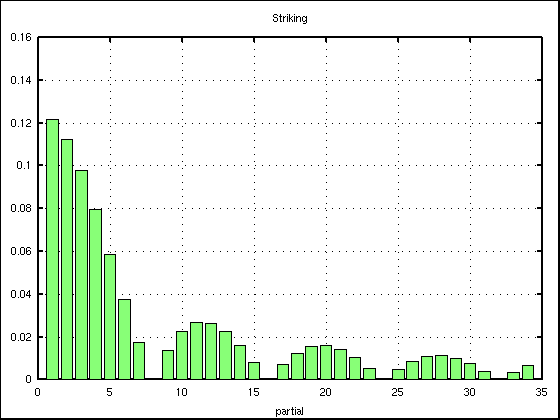
まず 周波数分布を示します。
左からクラヴィコード(Pushing)・ピアノ(Striking)・ハープ(Plucking)です。
横軸は倍音数で 縦軸は音量を表します。
ピアノとハープは打弦点を1/8に設定して計算しています。 クラヴィコードは打弦点が無い(0)ので消失する倍音はありません。
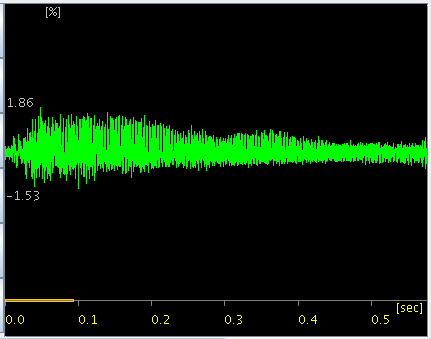
クラヴィコードの音とインハーモニシティを Java Pitch(JP)で見てみます。
(102KB)
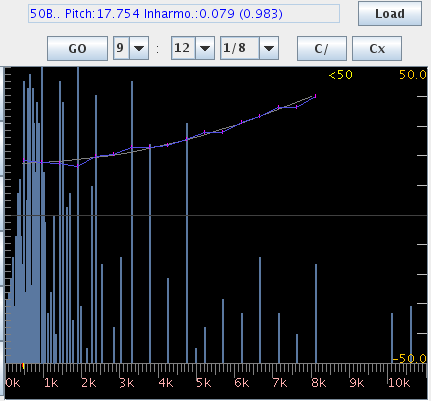
FFTのスペクトルを右へ行く程に少しづつレヴェルを上げて 倍音の分布を見てみます。
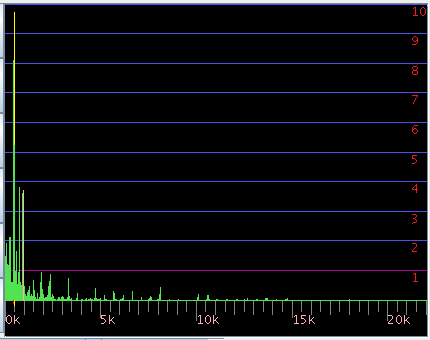
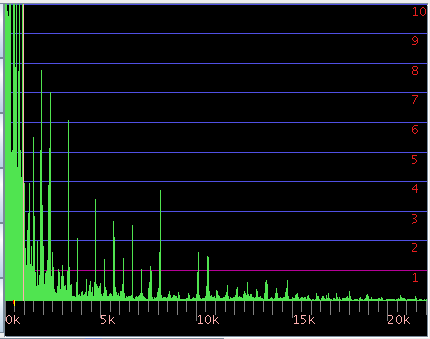
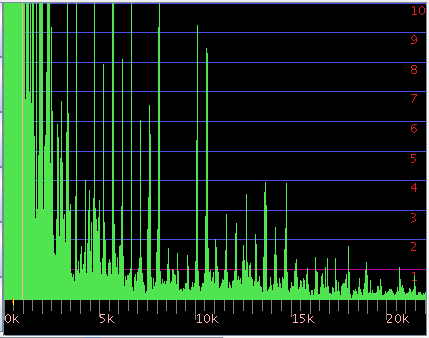
それをウェビュワー (Java Waviewer)の3DFFTの [Log](対数値)で見てみます。
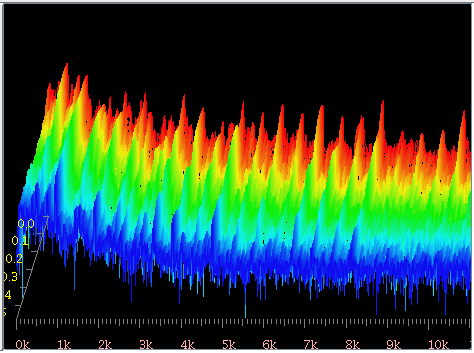
ピアノの音とインハーモニシティです。
低音では高倍音まで出ていますが
(A1キー)
高音になるほど倍音は少なくなります。
(123KB)
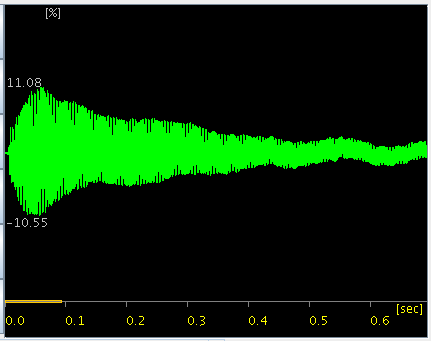
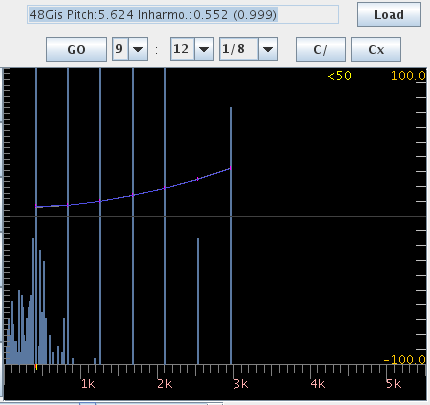
FFTのスペクトルを少しづつレヴェルを上げて 倍音の分布を見てみます。
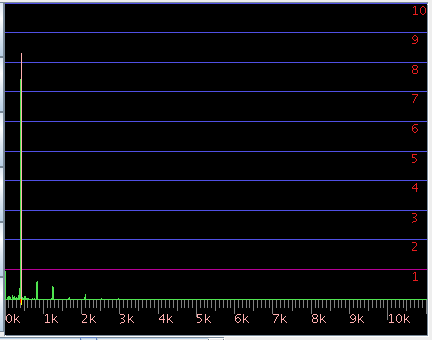
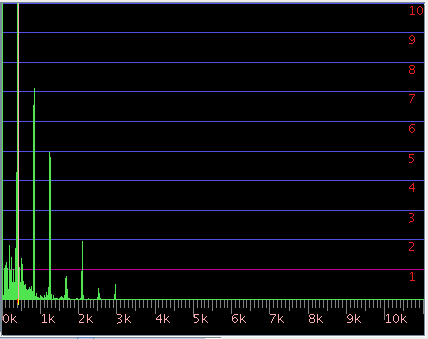
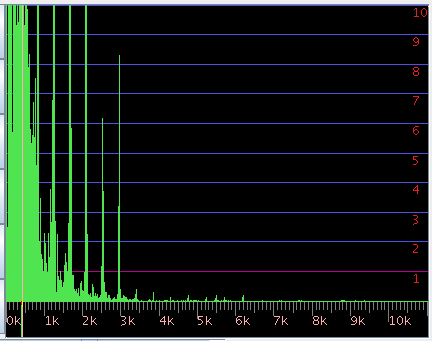
3DFFTで見てみます。
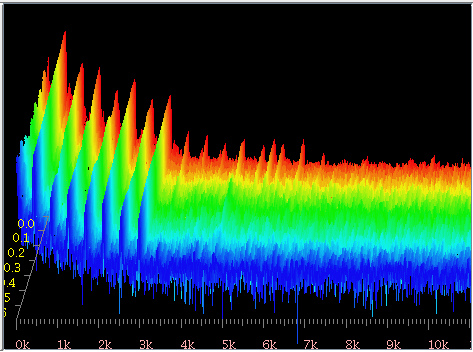
ハープの音とインハーモニシティです。
(152KB)
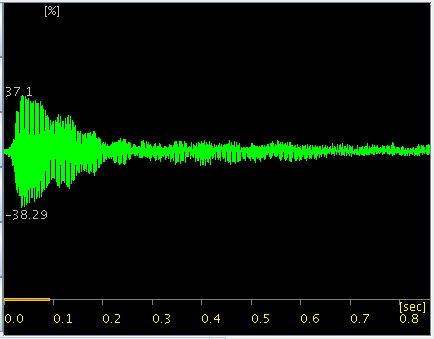
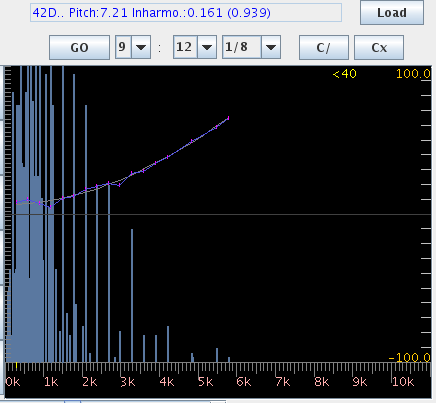
FFTのスペクトルを少しづつレヴェルを上げて 倍音の分布を見てみます。
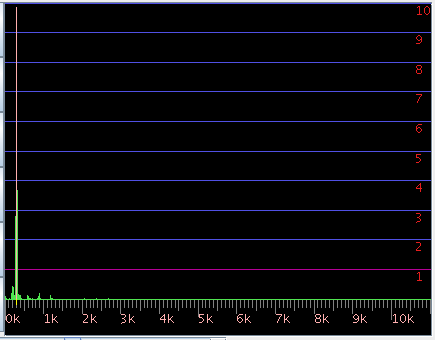
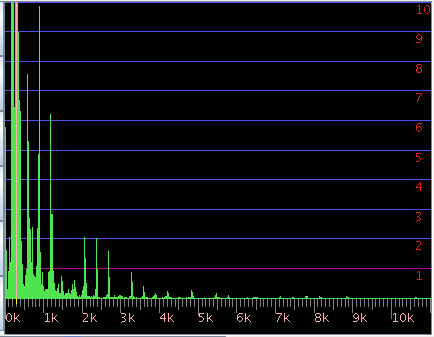
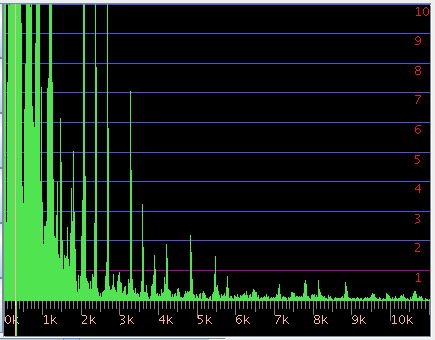
3DFFTで見てみます。
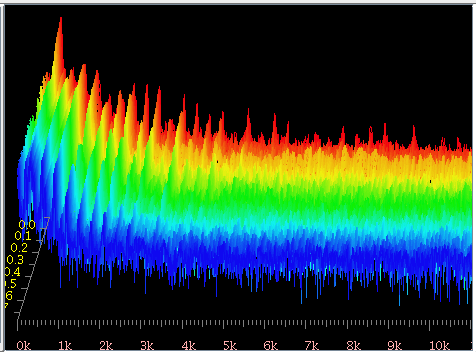
クラヴィコードの音量は小さいものの 倍音は豊かにある事が分かります。
