HTML5版の例をHTML5版へ移動しました。
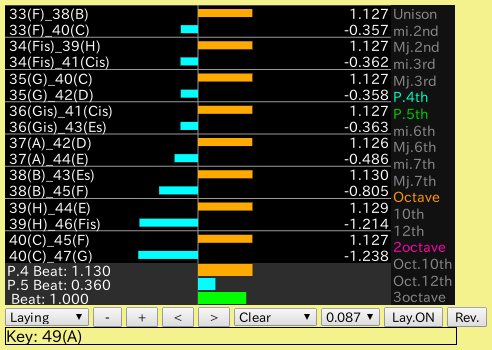
HTML5版です。
巻線部は 1(A)〜28(C)・傾き(曲線) 0.05
芯線部は 49(A)のインハーモニシティ値 0.55・傾き(直線) 0.087の
シミュレーションピアノです。
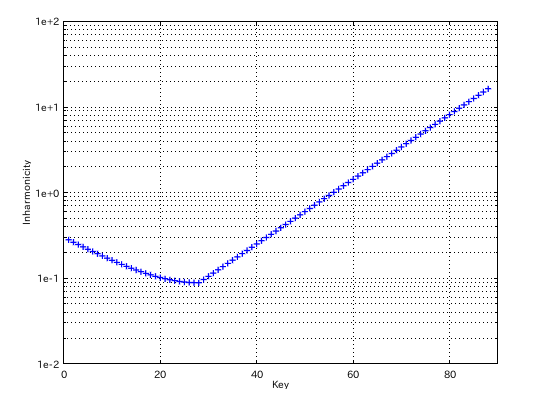
始めにセント値は 0のままの平均律として置きます。
(v0.2)(セント値には
インハーモニシティ値が加わっています。)
インハーモニシティ値を加え無くしました。
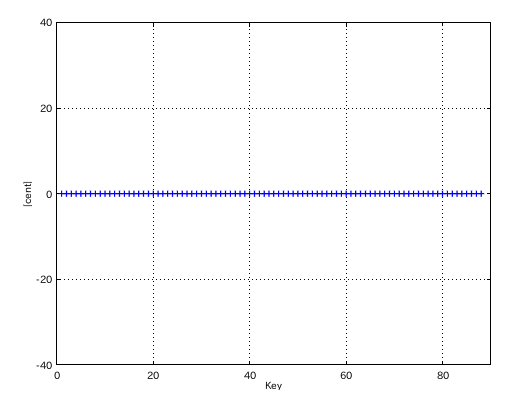
そこから ノンゼロ(NonZero)型で
Tuningシミュレーションを行ってみます。
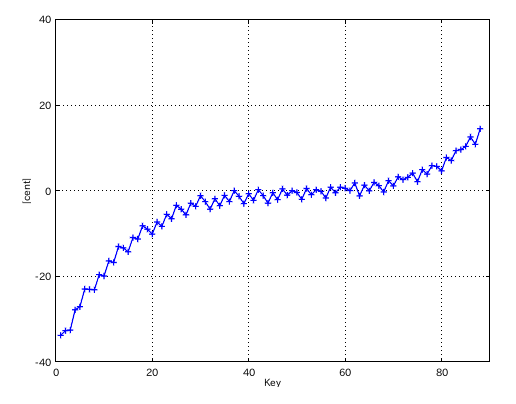
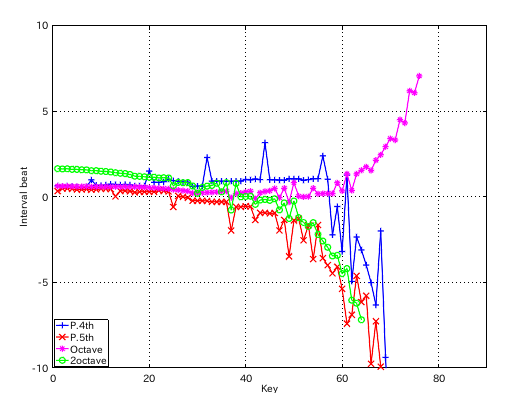
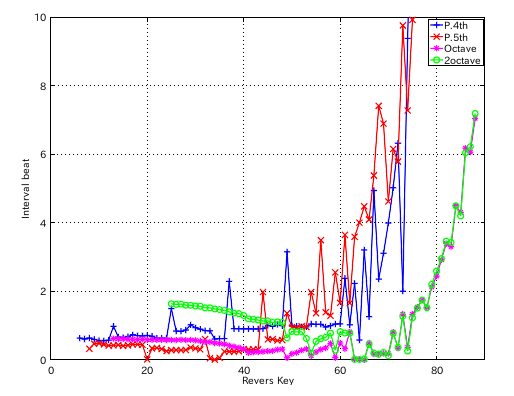
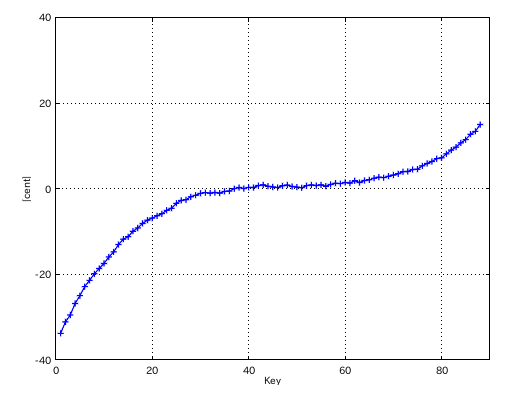
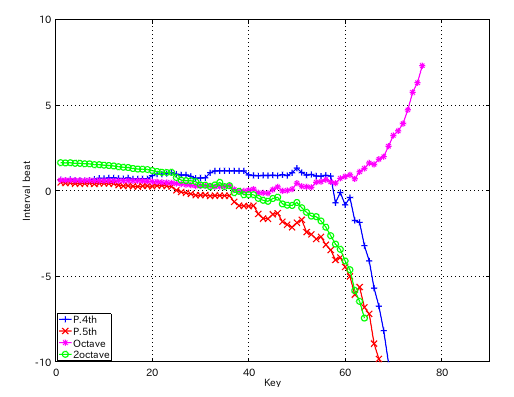
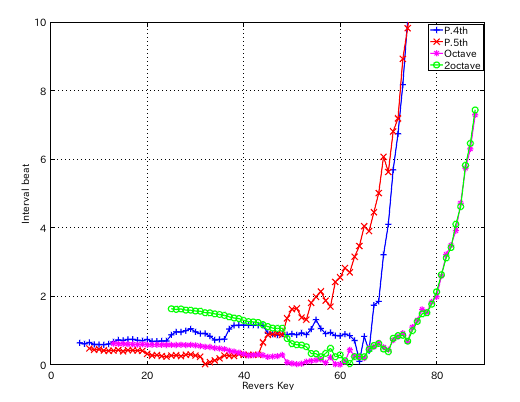
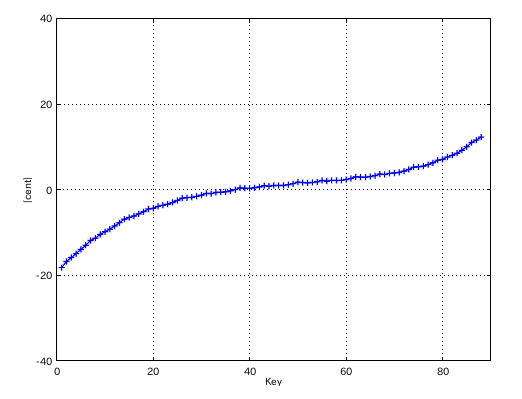
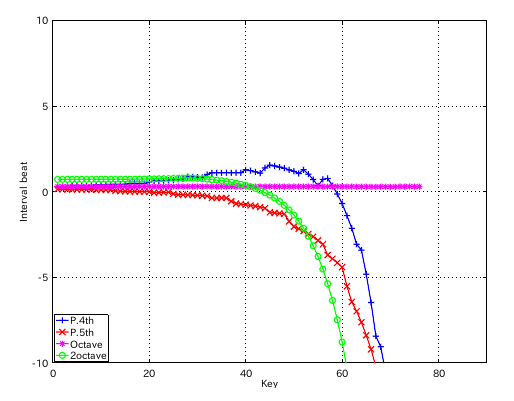
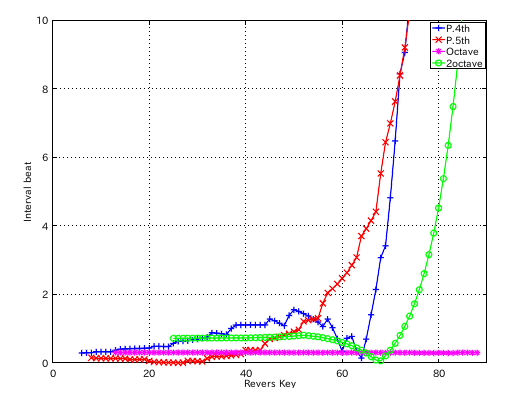
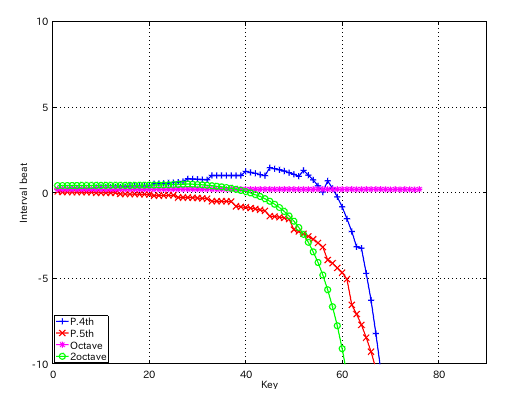
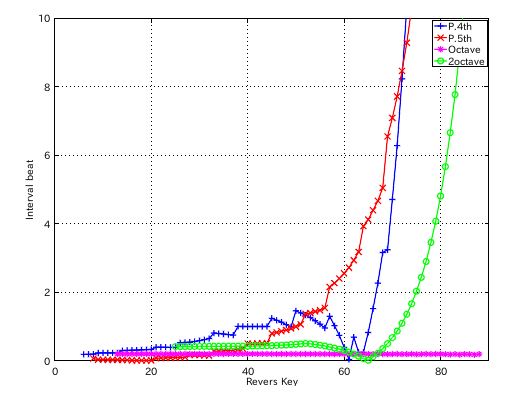
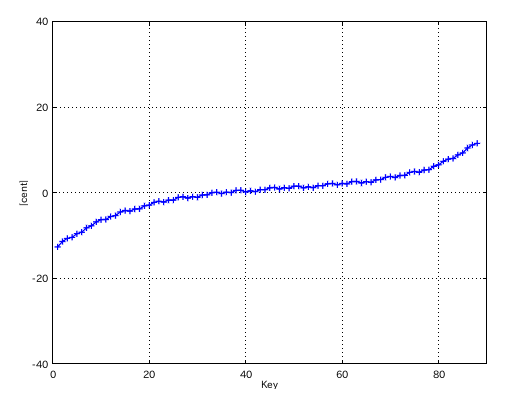
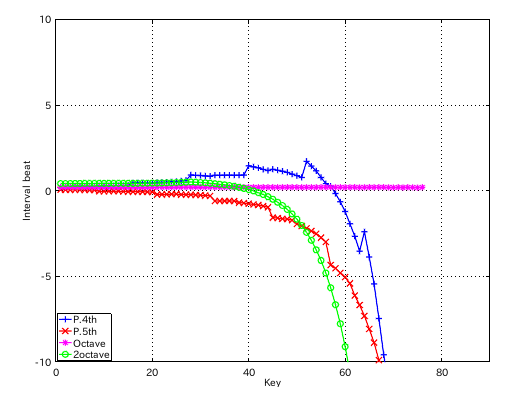
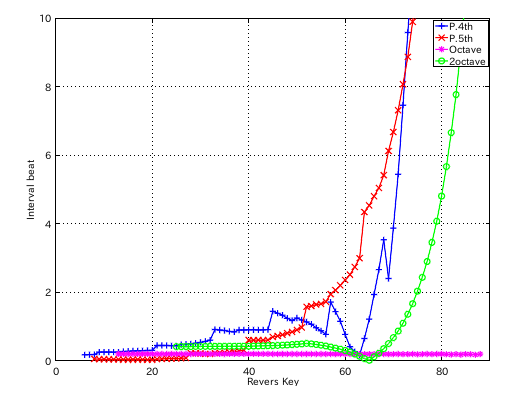
左からセント値・ビート・逆ビート順の図です。
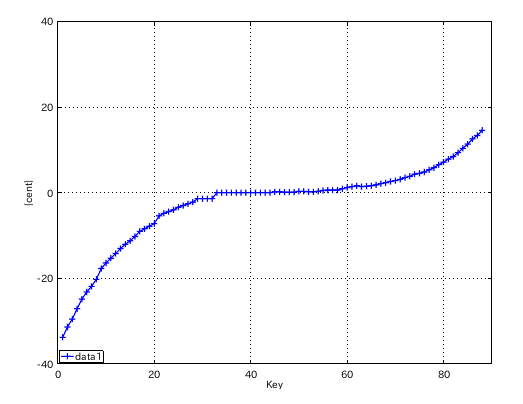
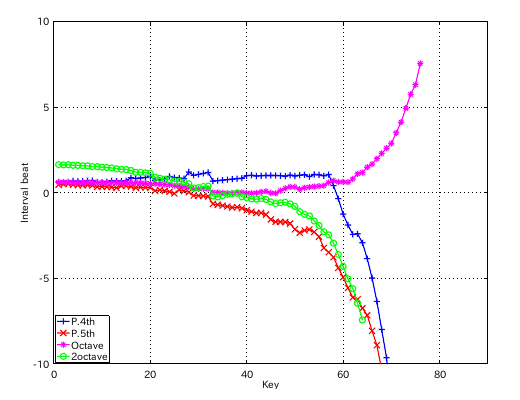
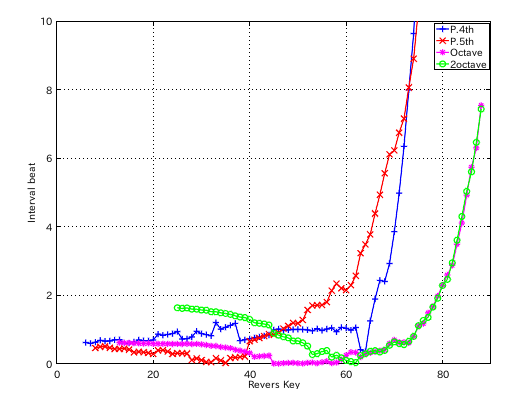
割振り範囲のキーの`うなり'の数です。
#: 4th 5th ---------------- 33: 0.674 -0.659 34: 0.703 -0.705 35: 0.732 -0.755 36: 0.761 -0.808 37: 0.789 -0.867 38: 0.816 -0.849 39: 0.842 -0.913 40: 0.987 -1.029 41: 1.015 -1.108 1: 37-42(4th) 0.789 2: 42-35(5th) 0.755 3: 35-40(4th) 0.732 4: 40-33(5th) 0.659 ...
割振りは行っていませんが それなりの曲線を示します。
次は 機械的に割振りに傾斜を付けてみます。
#: 4th 5th ---------------- 33: 0.842 -0.483 34: 0.881 -0.518 35: 0.921 -0.557 36: 0.961 -0.599 37: 1.001 -0.644 38: 1.041 -0.774 39: 1.080 -0.833 40: 0.999 -0.944 41: 1.028 -1.019 1: 37-42(4th) 1.001 2: 42-35(5th) 0.557 3: 35-40(4th) 0.921 4: 40-33(5th) 0.483 ...
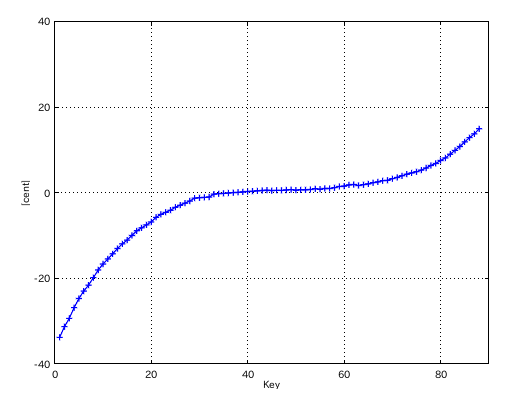
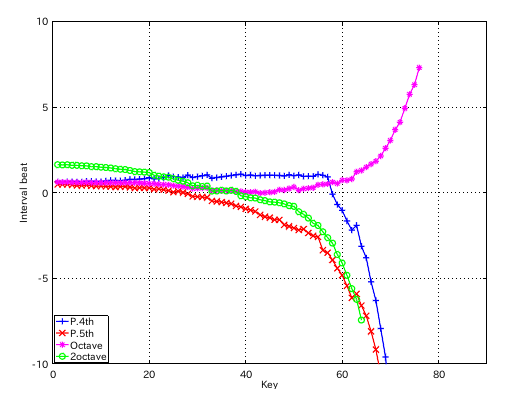
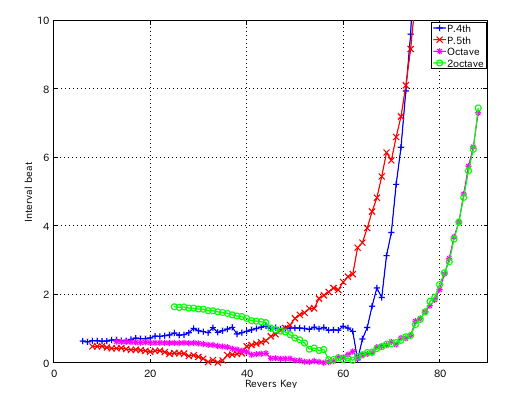
それでも それなりの曲線を示しています。
それでは 4度と5度の`うなり'の比を 3:1・4度の`うなり'を 1.0として
割振りをシミュレーションしてみます。
37(A)キーから 4度5度を繰り返して以下の数値となりました。
from Key-to Key = Beat ---------------------- 1: 37-42(4th) = 1.003 2: 42-35(5th) = 0.333 3: 35-40(4th) = 1.004 4: 40-33(5th) = 0.338 5: 33-38(4th) = 1.005 6: 38-43(4th) = 1.010 7: 43-36(5th) = 0.333 8: 36-41(4th) = 1.000 9: 41-34(5th) = 0.339 10: 34-39(4th) = 1.002 11: 39-44(4th) = 1.001 12: 44-37(5th) = 1.278
12番目の 5度(44-37)は 始まりの 37キーに戻って
割切れたかどうかを確認しています。
ここでは他の 5度より 4倍にもなっています。
上記の数値を キーの順に並べてみます。
#: 4th 5th ---------------- 33: 1.005 -0.338 34: 1.002 -0.339 35: 1.004 -0.333 36: 1.000 -0.333 37: 1.003 -1.278 38: 1.010 -0.733 39: 1.001 -0.739 40: 1.015 -0.708 41: 0.993 -0.720
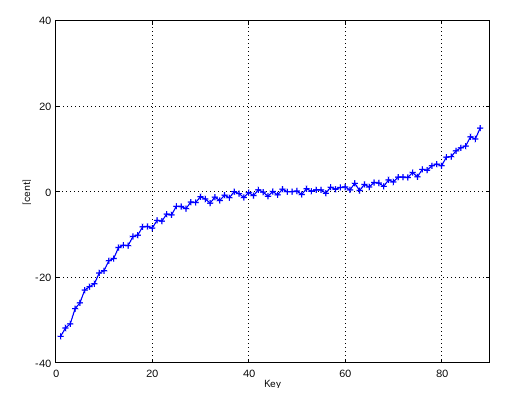
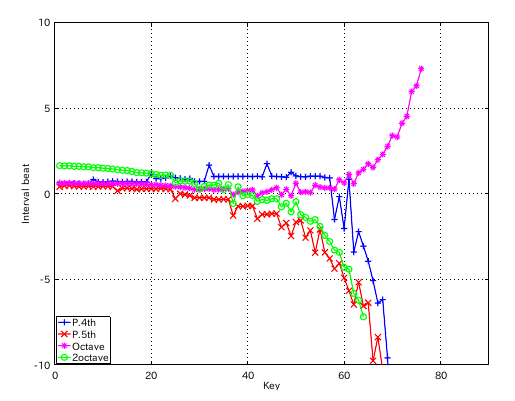
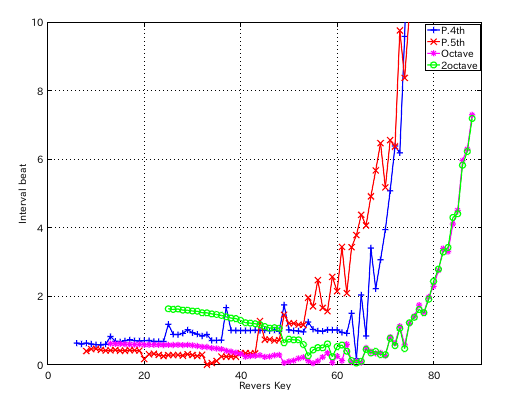
4度の`うなり'の数を 0.9にしてみます。
from Key-to Key = Beat ---------------------- 1: 37-42(4th) = 0.901 2: 42-35(5th) = 0.306 3: 35-40(4th) = 0.904 4: 40-33(5th) = 0.302 5: 33-38(4th) = 0.907 6: 38-43(4th) = 0.902 7: 43-36(5th) = 0.304 8: 36-41(4th) = 0.904 9: 41-34(5th) = 0.301 10: 34-39(4th) = 0.907 11: 39-44(4th) = 0.909 00: 44-37(5th) = 1.979 #: 4th 5th ---------------- 33: 0.907 -0.302 34: 0.907 -0.301 35: 0.904 -0.306 36: 0.904 -0.304 37: 0.901 -1.978 38: 0.902 -0.595 39: 0.909 -0.601 40: 1.003 -0.562 41: 0.979 -0.575
最後の 5度(44-37)は 1.979と増加しています。
4度の`うなり'の数が 1.3ではどうでしょう。
from Key-to Key = Beat ---------------------- 1: 37-42(4th) = 1.309 2: 42-35(5th) = 0.435 3: 35-40(4th) = 1.304 4: 40-33(5th) = 0.435 5: 33-38(4th) = 1.305 6: 38-43(4th) = 1.304 7: 43-36(5th) = 0.435 8: 36-41(4th) = 1.301 9: 41-34(5th) = 0.436 10: 34-39(4th) = 1.305 11: 39-44(4th) = 1.302 12: 44-37(5th) = -0.850 #: 4th 5th ----------------- 33: 1.305 -0.435 34: 1.305 -0.436 35: 1.304 -0.435 36: 1.301 -0.435 37: 1.309 0.850 38: 1.304 -1.155 39: 1.302 -1.170 40: 1.027 -1.145 41: 0.994 -1.165
最後の 5度(44-37)は -0.85と少な過ぎます。
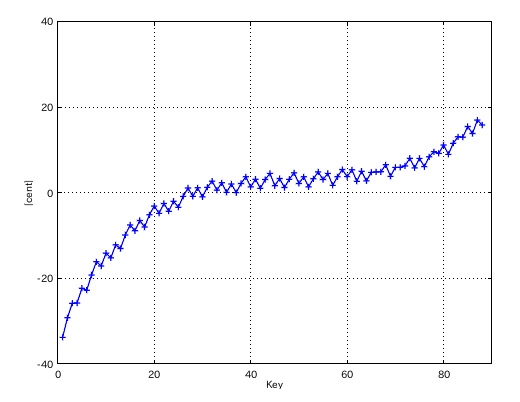
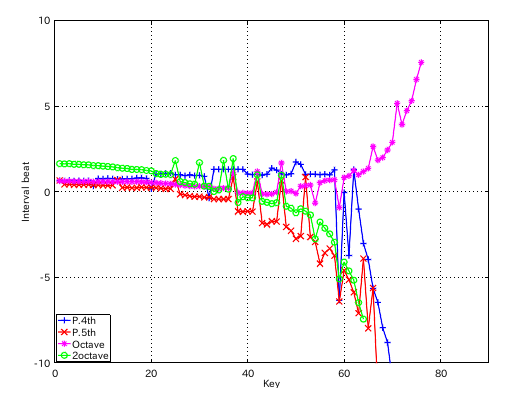
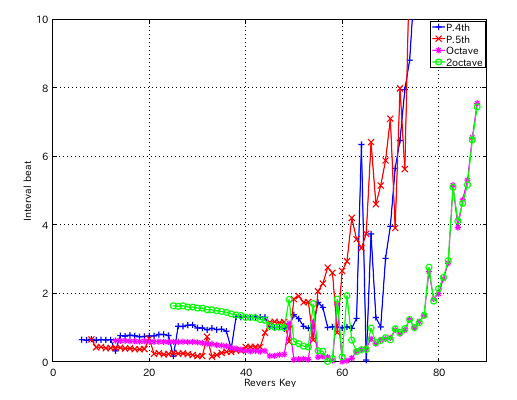
そして 4度の`うなり'の数が 1.125でだいたい割切れます。
from Key-to Key = Beat --------------------- 1: 37-42(4th) = 1.125 2: 42-35(5th) = 0.381 3: 35-40(4th) = 1.131 4: 40-33(5th) = 0.375 5: 33-38(4th) = 1.127 6: 38-43(4th) = 1.130 7: 43-36(5th) = 0.377 8: 36-41(4th) = 1.126 9: 41-34(5th) = 0.378 10: 34-39(4th) = 1.131 11: 39-44(4th) = 1.128 12: 44-37(5th) = 0.394 #: 4th 5th ---------------- 33: 1.127 -0.375 34: 1.131 -0.378 35: 1.131 -0.381 36: 1.126 -0.377 37: 1.125 -0.394 38: 1.130 -0.896 39: 1.128 -0.911 40: 1.027 -0.926 41: 1.006 -0.894
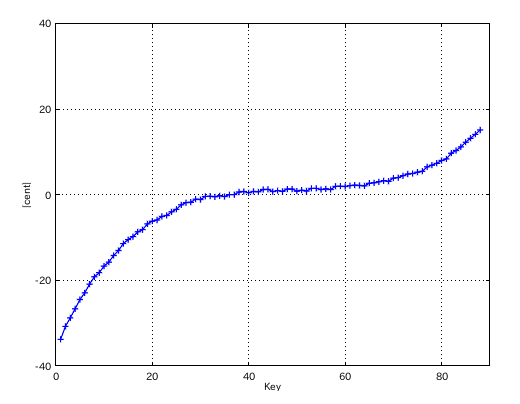
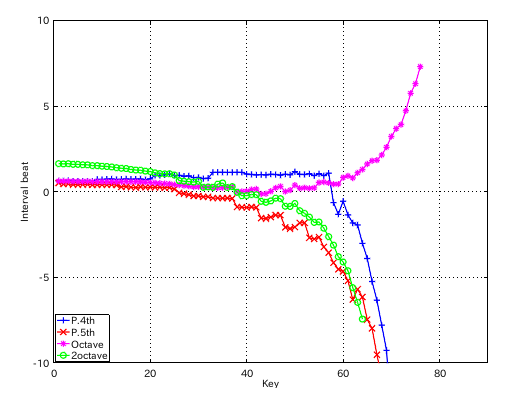
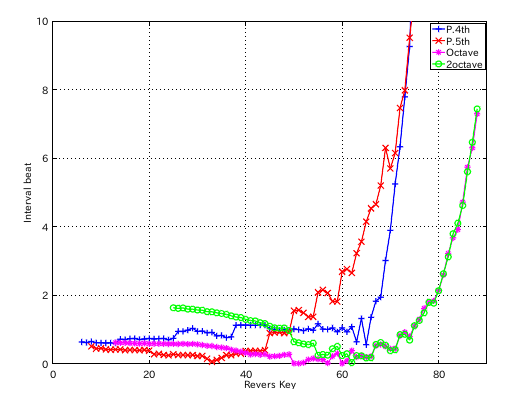
以上のように 割振りは凸凹でも伸長は出来ますが
`うなり'のずれは高音部程大きくなります。
そうした事から 割振りは 出来るだけ滑らかにする事が求められます。
そこで
さらにセント値の凹凸を無くす為に
"多項式近似"計算(polyfit)で"曲線の当てはめ(curve fitting)"を
行ってみます。
その結果(poly)を重ねたものと
結果(poly)のみを見てみます。
以下同様の polyfitは削除しました。
芯線部の傾き(直線)の違いではどうなるでしょう。 傾き(直線)を 0.075 にして見てみます。
from Key-to Key = Beat ---------------------- 1: 37-42(4th) = 1.134 2: 42-35(5th) = 0.375 3: 35-40(4th) = 1.132 4: 40-33(5th) = 0.377 5: 33-38(4th) = 1.129 6: 38-43(4th) = 1.131 7: 43-36(5th) = 0.381 8: 36-41(4th) = 1.131 9: 41-34(5th) = 0.376 10: 34-39(4th) = 1.129 11: 39-44(4th) = 1.134 12: 44-37(5th) = 0.074 #: 4th 5th ---------------- 33: 1.129 -0.377 34: 1.129 -0.376 35: 1.132 -0.375 36: 1.131 -0.381 37: 1.134 -0.074 38: 1.131 -0.892 39: 1.134 -0.912 40: 1.012 -0.895 41: 0.968 -0.876
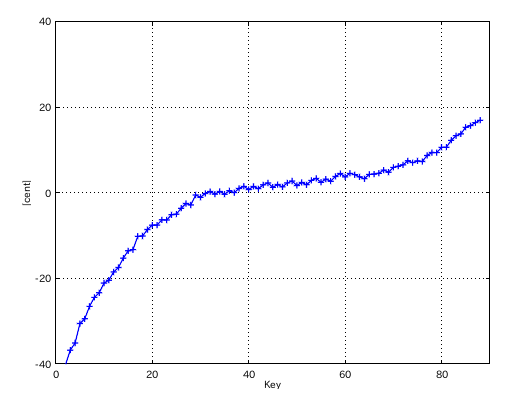
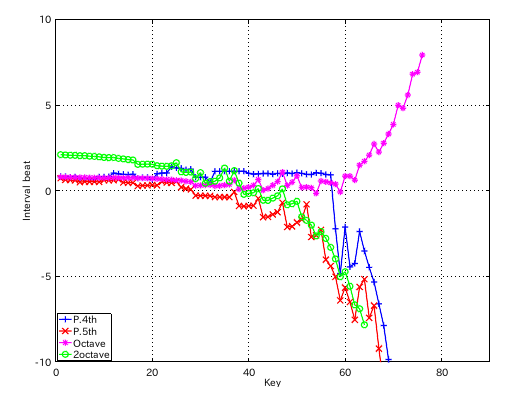
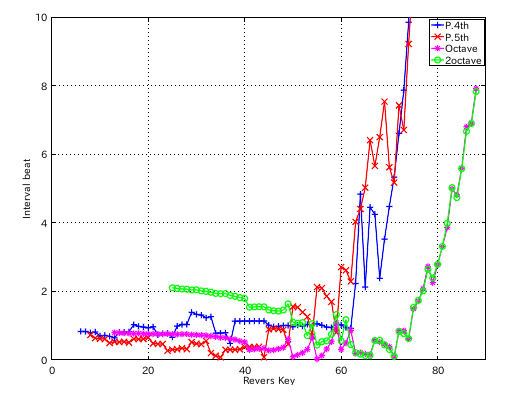
傾き(直線)を 0.095にしてみます。
from Key-to Key = Beat ---------------------- 1: 37-42(4th) = 1.134 2: 42-35(5th) = 0.377 3: 35-40(4th) = 1.130 4: 40-33(5th) = 0.375 5: 33-38(4th) = 1.127 6: 38-43(4th) = 1.133 7: 43-36(5th) = 0.378 8: 36-41(4th) = 1.130 9: 41-34(5th) = 0.377 10: 34-39(4th) = 1.127 11: 39-44(4th) = 1.127 12: 44-37(5th) = 0.560 #: 4th 5th -------------------- 33: 1.127 -0.375 34: 1.127 -0.377 35: 1.130 -0.377 36: 1.130 -0.378 37: 1.134 -0.560 38: 1.133 -0.932 39: 1.127 -0.937 40: 0.995 -0.905 41: 0.980 -0.915
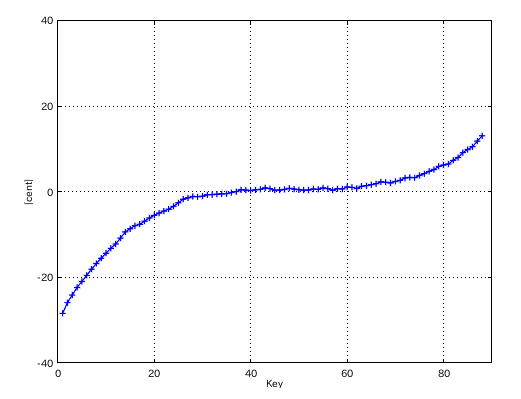
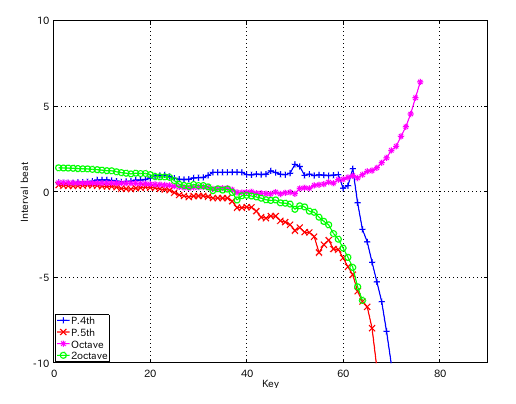
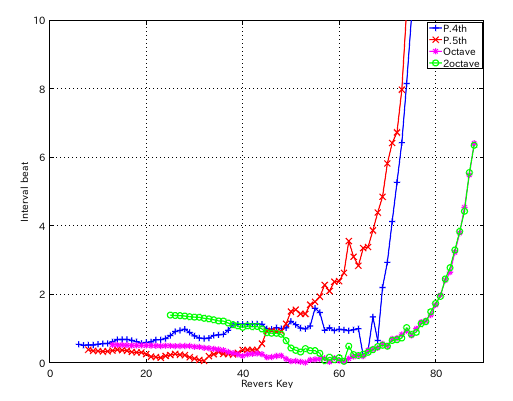
49(A)キーのインハーモニシティ値の違いではどうなるでしょう。 0.55から 0.45にしてみます。
from Key-to Key = Beat ---------------------- 1: 37-42(4th) = 1.132 2: 42-35(5th) = 0.378 3: 35-40(4th) = 1.132 4: 40-33(5th) = 0.380 5: 33-38(4th) = 1.131 6: 38-43(4th) = 1.129 7: 43-36(5th) = 0.379 8: 36-41(4th) = 1.130 9: 41-34(5th) = 0.376 10: 34-39(4th) = 1.130 11: 39-44(4th) = 1.132 12: 44-37(5th) = 0.463 #: 4th 5th -------------------- 33: 1.131 -0.380 34: 1.130 -0.376 35: 1.132 -0.378 36: 1.130 -0.379 37: 1.132 -0.463 38: 1.129 -0.935 39: 1.132 -0.942 40: 0.999 -0.910 41: 0.969 -0.922
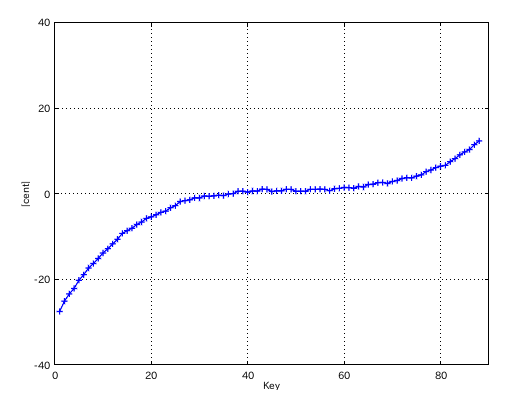
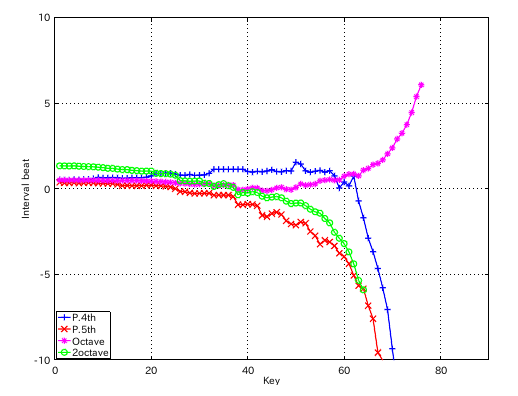
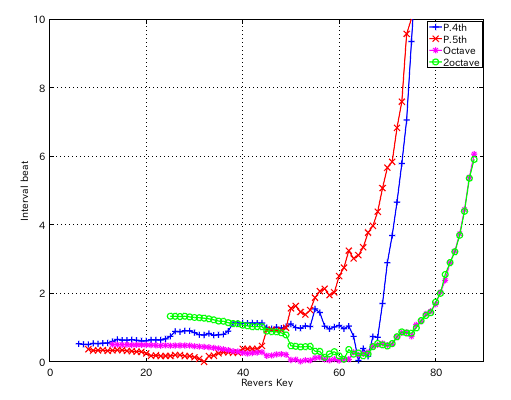
インハーモニシティ値を 0.65にしてみます。
from Key-to Key = Beat ---------------------- 1: 37-42(4th) = 1.129 2: 42-35(5th) = 0.377 3: 35-40(4th) = 1.131 4: 40-33(5th) = 0.375 5: 33-38(4th) = 1.130 6: 38-43(4th) = 1.130 7: 43-36(5th) = 0.381 8: 36-41(4th) = 1.133 9: 41-34(5th) = 0.380 10: 34-39(4th) = 1.133 11: 39-44(4th) = 1.136 12: 44-37(5th) = 0.286 #: 4th 5th ---------------- 33: 1.130 -0.375 34: 1.133 -0.380 35: 1.131 -0.377 36: 1.133 -0.381 37: 1.129 -0.286 38: 1.130 -0.905 39: 1.136 -0.924 40: 1.006 -0.897 41: 0.978 -0.876
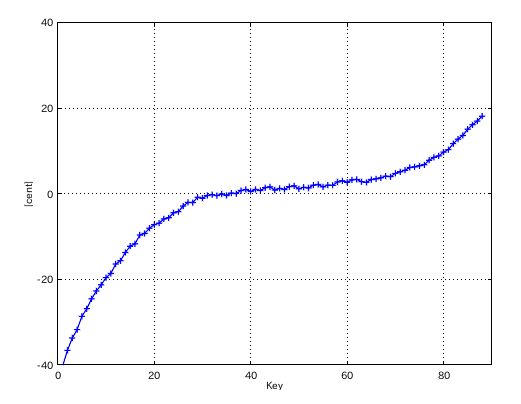
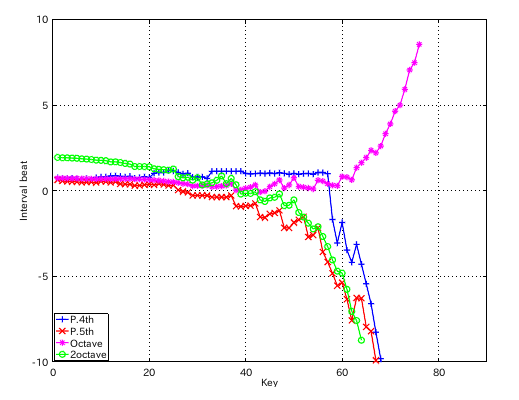
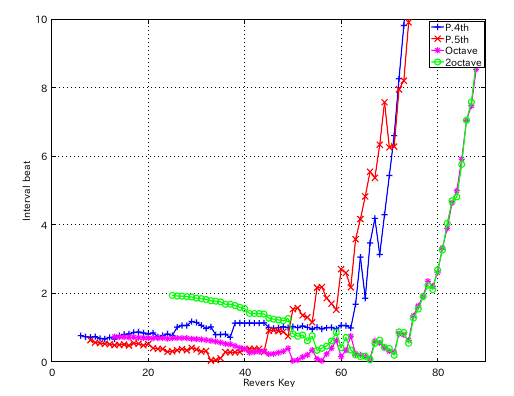
4度と5度の`うなり'の比を変えるとどうなるでしょう。 `うなり'の比を 2:1にしてみます。
from Key-to Key = Beat ---------------------- 1: 37-42(4th) 1.003 2: 42-35(5th) 0.503 3: 35-40(4th) 1.004 4: 40-33(5th) 0.502 5: 33-38(4th) 1.005 6: 38-43(4th) 1.000 7: 43-36(5th) 0.506 8: 36-41(4th) 1.001 9: 41-34(5th) 0.500 10: 34-39(4th) 1.003 11: 39-44(4th) 1.002 12: 44-37(5th) 0.516 #: 4th 5th -------------------- 33: 1.005 -0.502 34: 1.003 -0.500 35: 1.004 -0.503 36: 1.001 -0.506 37: 1.003 -0.516 38: 1.000 -0.977 39: 1.002 -0.955 40: 0.977 -0.936 41: 0.992 -0.962
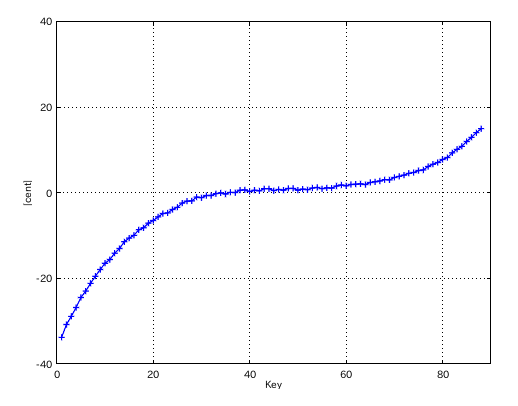
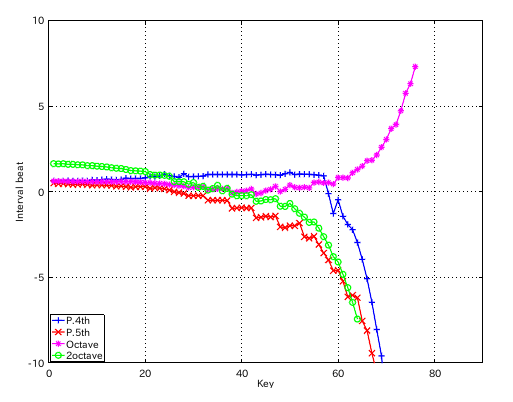
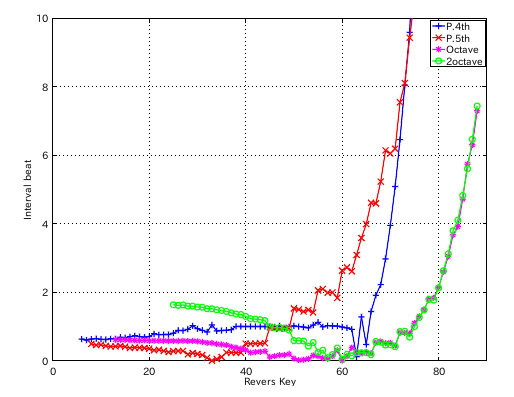
次は 4:1の比にしてみます。
from Key-to Key = Beat ---------------------- 1: 37-42(4th) = 1.156 2: 42-35(5th) = 0.293 3: 35-40(4th) = 1.158 4: 40-33(5th) = 0.290 5: 33-38(4th) = 1.151 6: 38-43(4th) = 1.151 7: 43-36(5th) = 0.290 8: 36-41(4th) = 1.155 9: 41-34(5th) = 0.288 10: 34-39(4th) = 1.156 11: 39-44(4th) = 1.151 12: 44-37(5th) = 0.653 #: 4th 5th ---------------- 33: 1.151 -0.290 34: 1.156 -0.288 35: 1.158 -0.293 36: 1.155 -0.290 37: 1.156 -0.653 38: 1.151 -0.879 39: 1.151 -0.893 40: 0.918 -0.908 41: 0.890 -0.874
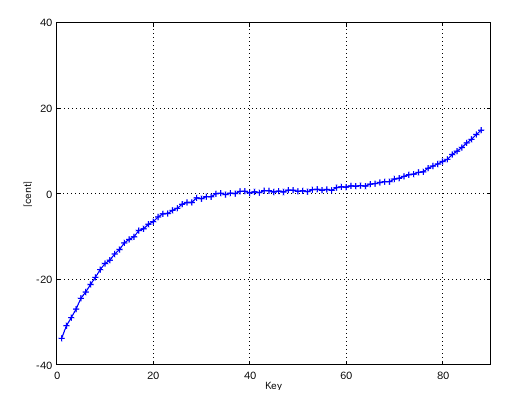
次は 3:2の比にしてみます。
from Key-to Key = Beat ---------------------- 1: 37-42(4th) = 0.901 2: 42-35(5th) = 0.605 3: 35-40(4th) = 0.904 4: 40-33(5th) = 0.605 5: 33-38(4th) = 0.900 6: 38-43(4th) = 0.903 7: 43-36(5th) = 0.600 8: 36-41(4th) = 0.905 9: 41-34(5th) = 0.602 10: 34-39(4th) = 0.900 11: 39-44(4th) = 0.911 12: 44-37(5th) = 0.607 #: 4th 5th ---------------- 33: 0.900 -0.605 34: 0.900 -0.602 35: 0.904 -0.605 36: 0.905 -0.600 37: 0.901 -0.607 38: 0.903 -0.994 39: 0.911 -0.981 40: 1.000 -0.973 41: 1.004 -0.963
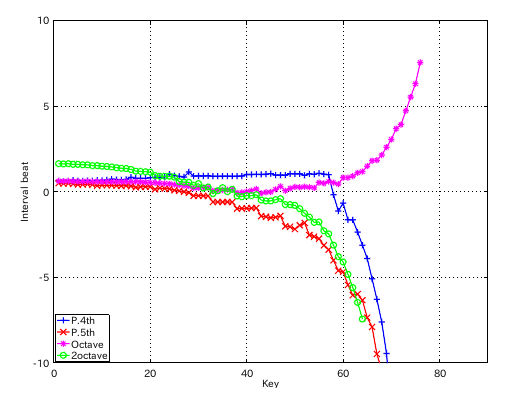
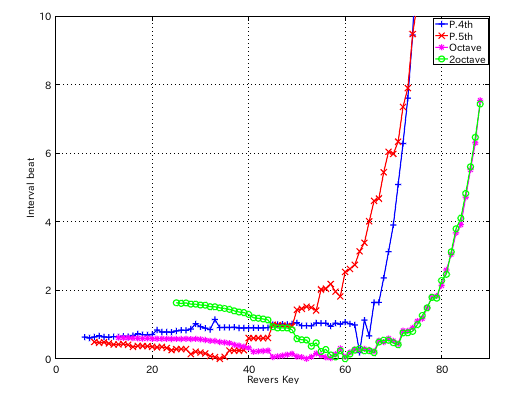
次は 1:1の比にしてみます。
from Key-to Key = Beat ---------------------- 1: 37-42(4th) = 0.738 2: 42-35(5th) = 0.734 3: 35-40(4th) = 0.732 4: 40-33(5th) = 0.732 5: 33-38(4th) = 0.730 6: 38-43(4th) = 0.730 7: 43-36(5th) = 0.736 8: 36-41(4th) = 0.732 9: 41-34(5th) = 0.731 10: 34-39(4th) = 0.737 11: 39-44(4th) = 0.739 12: 44-37(5th) = 0.950 #: 4th 5th ---------------- 33: 0.730 -0.732 34: 0.737 -0.731 35: 0.732 -0.734 36: 0.732 -0.736 37: 0.738 -0.950 38: 0.730 -0.987 39: 0.739 -0.990 40: 1.011 -0.983 41: 1.002 -0.982
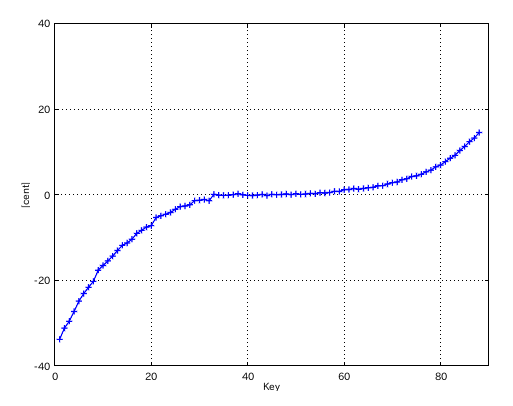
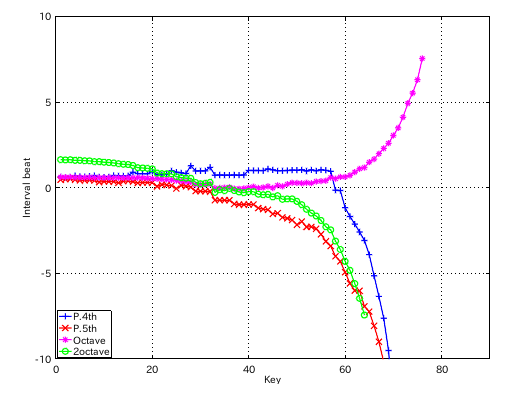
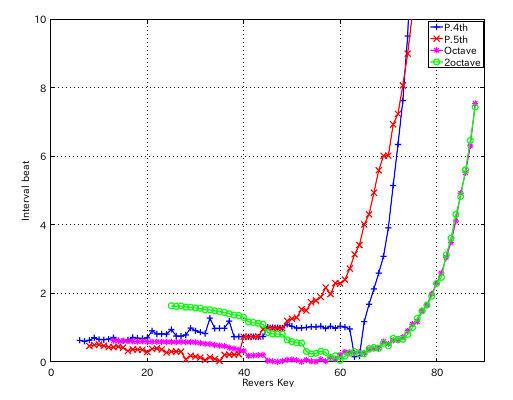
4度と5度の`うなり'の比の違いを オクターブで合わせる方法で拡張を行ってみます。
3:1 の場合です。
2:1 の場合です。
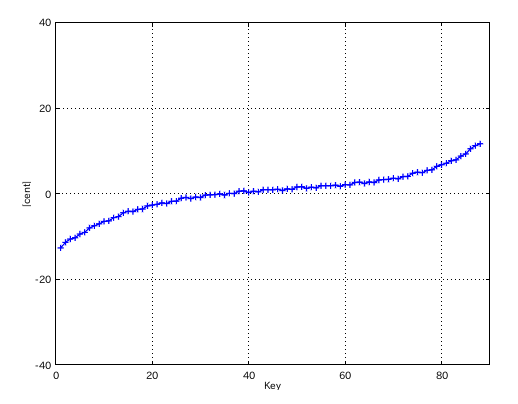
1:1 の場合です。
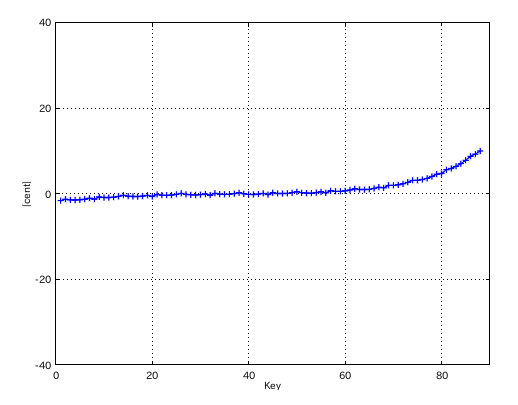
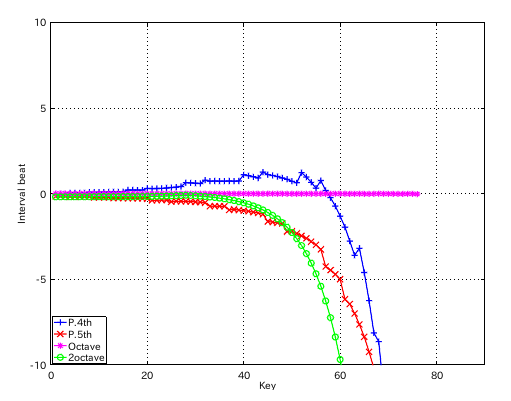
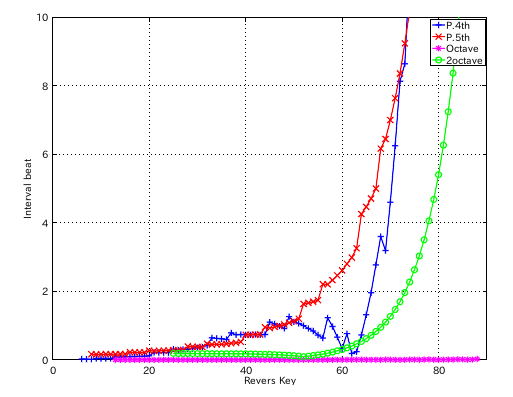
4:1 の場合です。
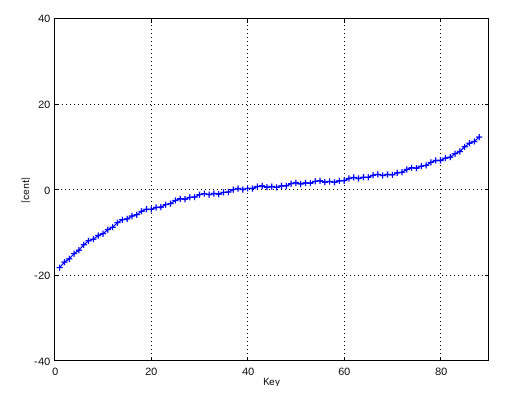
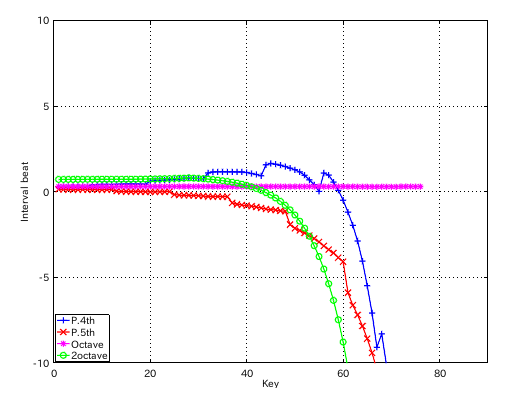
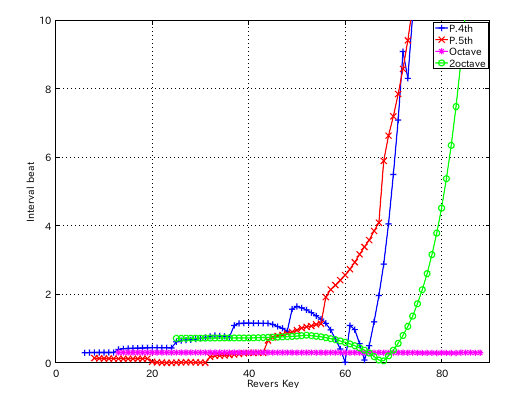
3:2 の場合です。
これを始めるまでは 実際の調律に近付けば 最適の値が得られるのでは と思っていました。
しかし結果的には 割振りの4度対5度の比は自由で オクターブでの拡張も `うなり'は 0でも 0でなくても Tuningの出来る可能性があります。
それはつまり インハーモニシティでは ピアノの数だけピアノの音があり Tuningでは 合わせる人の数だけ ピアノには音がある様に思われますが如何でしょうか?
参照〉Java調律シミュレーター (Java Tuning Simulator)
(変更履歴:

HTML5版です。