変更履歴:
v0.1.1['14/02/09]
HTML5版を追加しました。
cssファイルを追加しました。
v0.1['10/09/13]
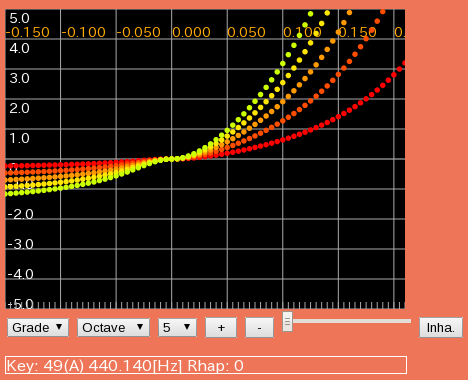
「インハーモニシティの曲線から調律曲線を求める (Inharmonicity curve to Tuning Curve)」では 傾き(Grade)を変えながらキー毎の`うなり'を見てみましたが それを数値計算ソフト「Octave」で行うと だいたい以下のようになります。
参照〉ピアノのための初級 Octaveプログラミング講座 (Octave)
function dispGrade(keys, inte)
global ML Pitch;
ML = log10(2)/1200;
Pitch = 440;
KB = 88;
woundw = 28; # 巻線数
inhar = 0.55; # A49のインハーモニシティ値
grade = -0.15:0.01:0.15;
multi = 1:3; # 倍音の範囲
ratio = Interval(inte);
ihs = []; # 先にgradeを作っておきます
for n = grade
ihs = [ihs; makeGrade(woundw, inhar, n)];
end
for k = keys
khi = k+inte;
if (khi > KB)
break;
end
ihlow = ihs(:,k)'; # 並び方を変えます
ihhi = ihs(:,khi)'; # 同上
be = [];
for m = multi
ra = [ratio(1:2)*m, inte];
bes = getGBeat(k, ihlow, ihhi, ra);
be = [be; bes];
end
plot(grade, be, '-@;;')
hold on
end
hold off
xlabel('Grade')
ylabel('beats')
end
function ih = makeGrade(ww, a49, gr)
x = [1:88]-ww;
if (gr < 0)
ih = 1./cosh(gr.*x);
else
ih = cosh(gr.*x);
end
df = a49/ih(49);
ih = ih.*df;
end
function beat = getGBeat(key, ihl, ihh, ratio)
freq1 = getGFrequ(key, ihl, ratio(1));
freq2 = getGFrequ(key+ratio(3), ihh, ratio(2));
beat = freq2-freq1;
end
function ifreq = getGFrequ(key, ih, multi)
freq = getFrequ(key).*multi;
ifreq = ctof(freq, calcInha(ih, multi));
end
function ih = calcInha(inh, multi)
ih = inh*multi*multi;
end
インハーモニシティの曲線の傾き(Grade)を -0.15〜0.15まで変化させるのでした。
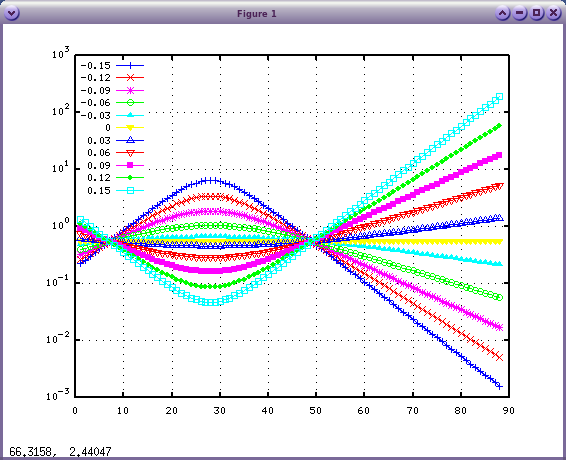
試しに A37のオクターブを見てみます。(3倍音までです)
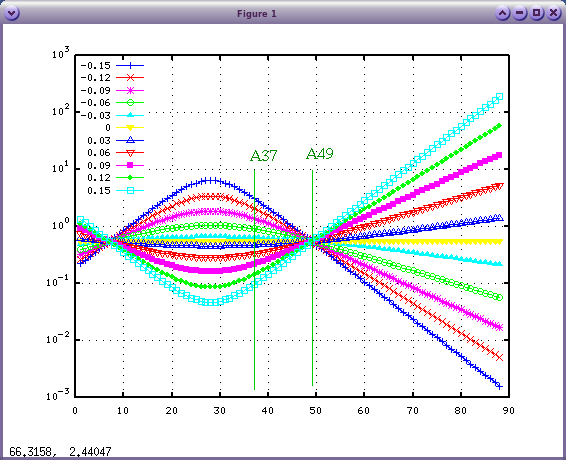
インハーモニシティ値・2:1の周波数・周波数差を取り出してみます。
傾き(Grade): A37 Inha.: A49 Inha.: A37x2 [Hz]: A49 [Hz]: 周波数差
------------------------------------------------------------------
-0.15 3.1235 0.55 443.19 440.14 -3.0471
-0.14 2.7389 0.55 442.79 440.14 -2.6535
-0.13 2.3975 0.55 442.44 440.14 -2.3043
-0.12 2.0948 0.55 442.13 440.14 -1.995
-0.11 1.8269 0.55 441.86 440.14 -1.7214
-0.1 1.5905 0.55 441.62 440.14 -1.4801
-0.09 1.3829 0.55 441.41 440.14 -1.2683
-0.08 1.2016 0.55 441.22 440.14 -1.0835
-0.07 1.0449 0.55 441.06 440.14 -0.92379
-0.06 0.91136 0.55 440.93 440.14 -0.78767
-0.05 0.79974 0.55 440.81 440.14 -0.67397
-0.04 0.70926 0.55 440.72 440.14 -0.58183
-0.03 0.63936 0.55 440.65 440.14 -0.51066
-0.02 0.58965 0.55 440.6 440.14 -0.46005
-0.01 0.5599 0.55 440.57 440.14 -0.42977
0 0.55 0.55 440.56 440.14 -0.41969
0.01 0.54027 0.55 440.55 440.14 -0.40979
0.02 0.51302 0.55 440.52 440.14 -0.38204
0.03 0.47313 0.55 440.48 440.14 -0.34145
0.04 0.4265 0.55 440.43 440.14 -0.29399
0.05 0.37825 0.55 440.38 440.14 -0.2449
0.06 0.33192 0.55 440.34 440.14 -0.19776
0.07 0.28949 0.55 440.29 440.14 -0.15459
0.08 0.25174 0.55 440.26 440.14 -0.11619
0.09 0.21875 0.55 440.22 440.14 -0.082632
0.1 0.19019 0.55 440.19 440.14 -0.053583
0.11 0.16558 0.55 440.17 440.14 -0.028555
0.12 0.1444 0.55 440.15 440.14 -0.0070205
0.13 0.12617 0.55 440.13 440.14 0.011521
0.14 0.11044 0.55 440.11 440.14 0.027513
0.15 0.096846 0.55 440.1 440.14 0.04134
--------------------------------------------------------------------
A49は 起点ですので 常に一定です。
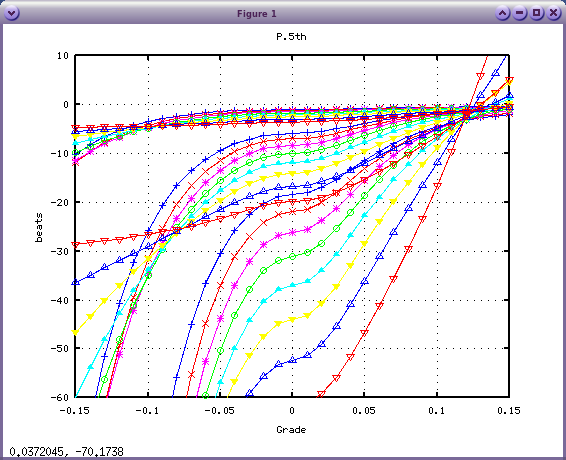
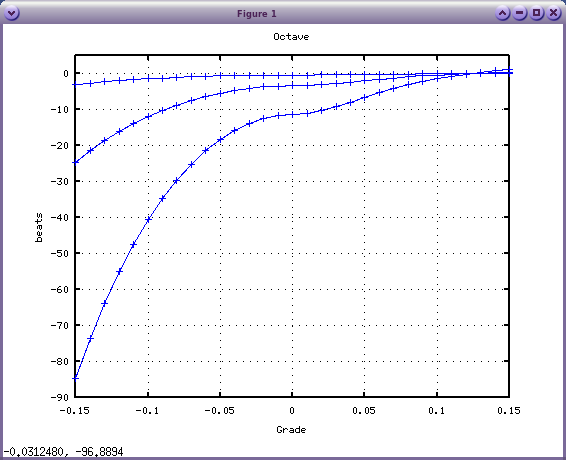
では 傾き(Grade)を変えながら オクターブの`うなり'を C(28)キーから 3キー毎に A(49)キーまでを 「Octave」で見てみます。
octave:1> dispGrade([28:3:49], 12)
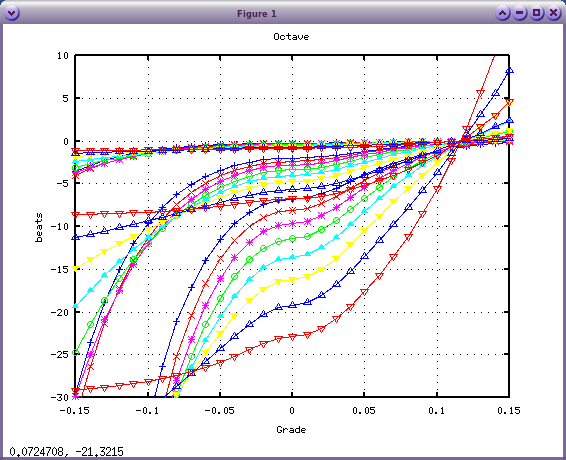
`うなり'が 0になる 傾き(Grade)の転換点は 0.115辺りです。
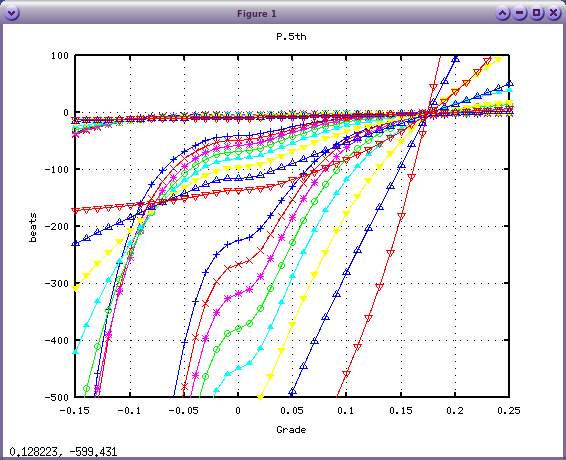
calcInha.mの内容を 以下の様に変更してみます。(x3)
ih = inh*multi*multi*multi;
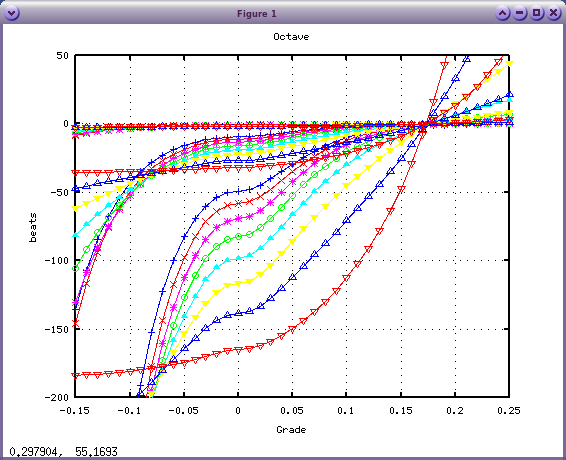
転換点は 0.17〜0.18に移動しています。
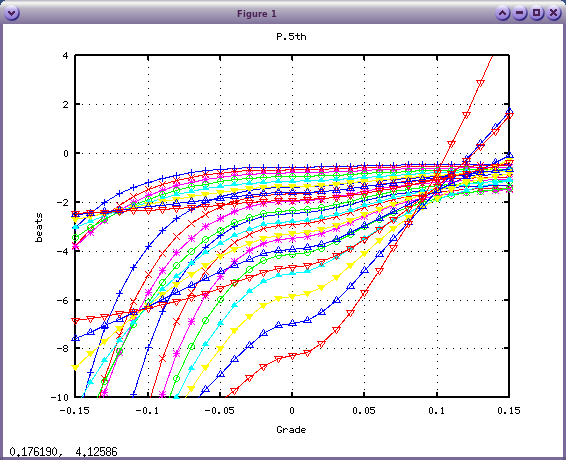
では calcInha.mを以下のように変更してみます。(x1)
ih = inh*multi;
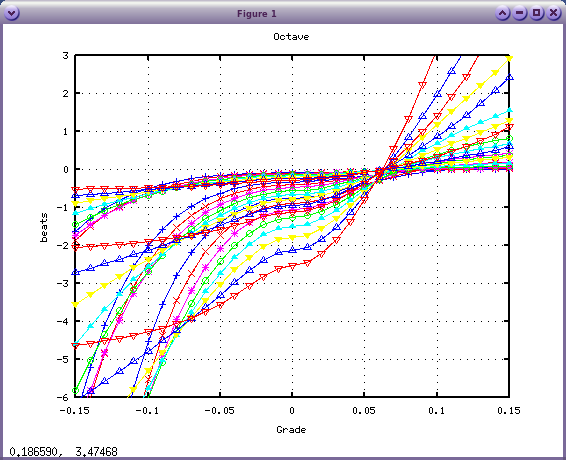
今度は 0.06〜0.07に移動しました。
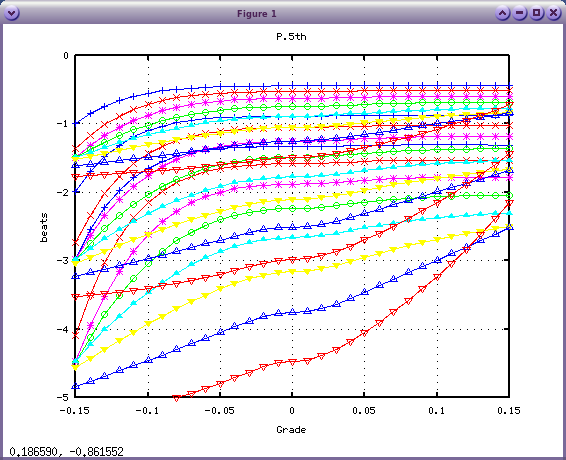
最後に calcInha.mを以下のように変更してみます。(x0)
ih = inh;
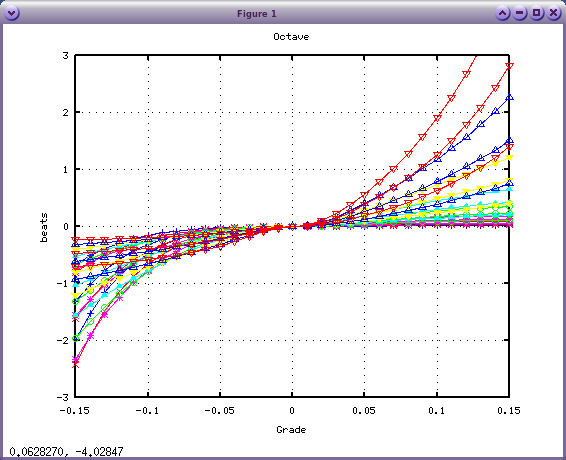
傾き(Grade)が 0の時
つまり、全てのキーでインハーモニシティ値が同じ場合は
オクターブでは 全ての倍音の`うなり'が 0になります。
つまりそれは "平均律" の事になります。
以上の変更は 机上の空論ですが この様にインハーモニシティ値の計算は "倍数 x 倍数"と言う部分のみに由来している事が分かります。

HTML5です。
ただし 4度・5度は 0セントでは"ずれ"があるので
同じにはなりません。
4度で x2 x3 x1 x0の順です。
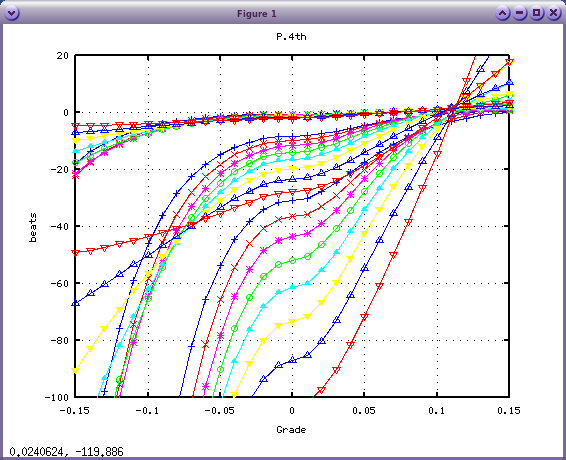
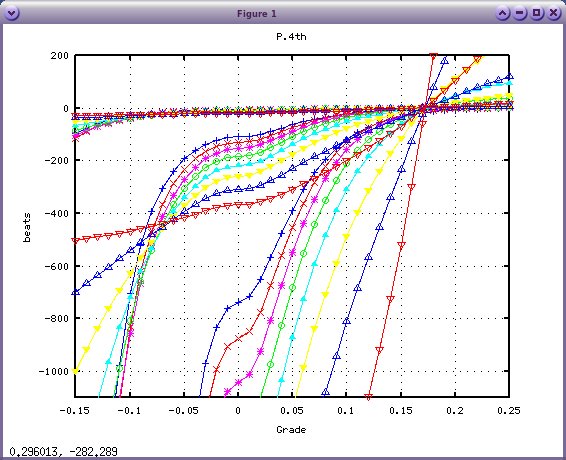
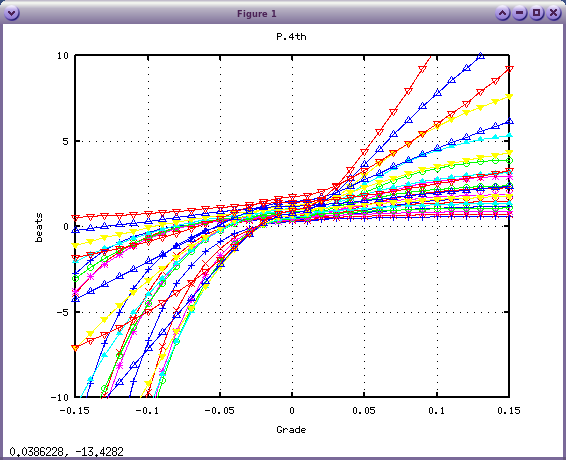
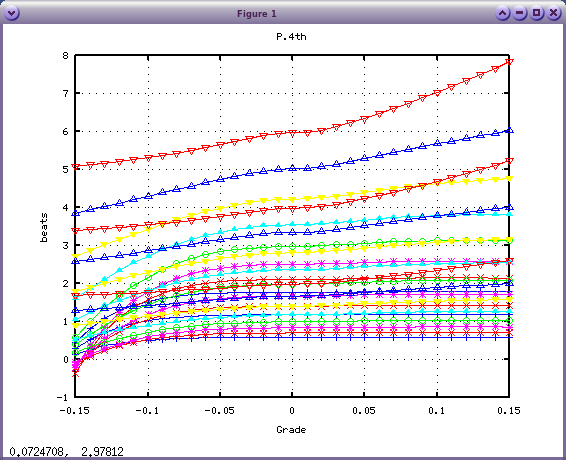
5度で x2 x3 x1 x0の順です。