調律のシミュレーション (Tuning Simulation) v0.1.2
インハーモニシティ値から調律をシミュレーションする方法を試してみます。
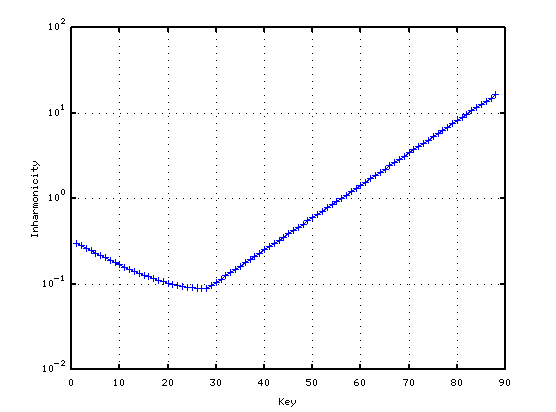
例えば芯線部は A(49)のインハーモニシティ値 0.55・傾き(直線) 0.087、
巻線部は A(1)〜C(28)・傾き(曲線) 0.07
としたインハーモニシティ値を用意します。
(v0.1.2)「調律曲線を求める一つの試み
(Tuning Curve Pursuits)」以後
セント値表示からインハーモニシティ値を加え無くする様になりましたが
ここでは初期の考え方の記録でもありますので
そのままにしてあります。
調律曲線グラフの高音部分を多少下げて 見て頂ければと思います。
参照>
Java 調律シミュレーター (Java Tuning Simulator)
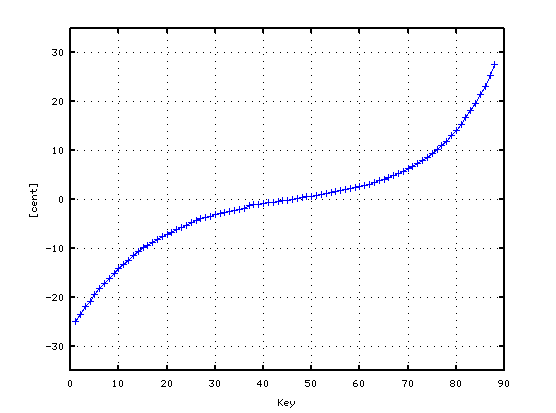
ここでの Tuningのシミュレーションは A(49)を中心にA(61)とA(37)まで
等間隔でセント値を加えて直線の傾きを作ってから
オクターブ(純正4度・純正5度...)などの音程で
上下のキーの周波数を変えて行き
目的の`うなり'の値にすると言う単純な方法です。
初めは オクターブで`うなり'を 0.4にしています。
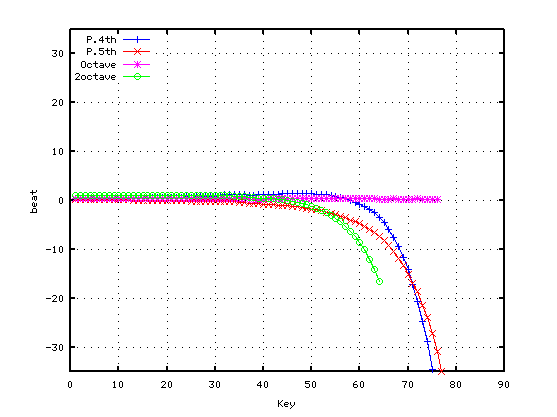
調律曲線は±30[cent]内で 適度なカーブを描いています。
その時の 純正4度・純正5度・オクターブ・2オクターブの
`うなり'を表示します。
(下の数値は 割振りの最初部分の`うなり'を示します。)
A(37)-D(42) 4th: 1.0858
G(35)-D(42) 5th: -0.3189
G(35)-C(40) 4th: 1.2077
F(33)-C(40) 5th: -0.1904
...
純正5度で`うなり'を 0.1とした場合です。
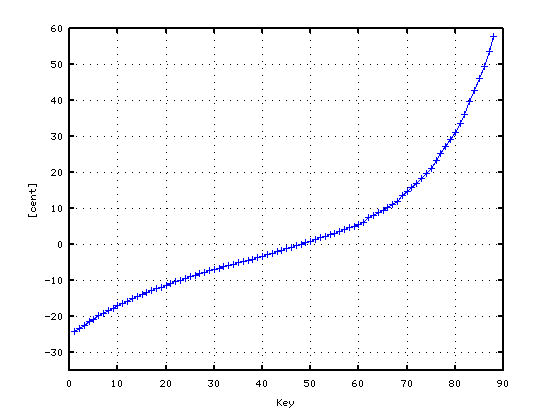
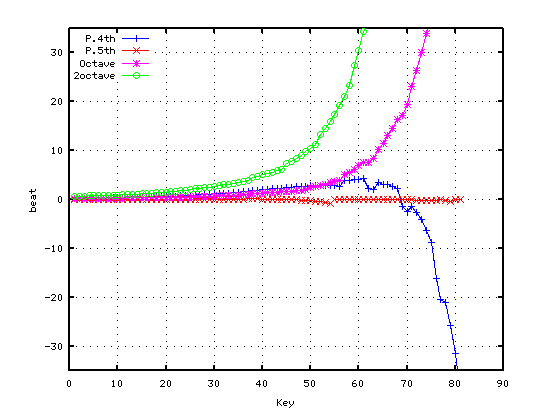
A(37)-D(42) 4th: 1.7620
G(35)-D(42) 5th: 0.0996
G(35)-C(40) 4th: 1.5226
F(33)-C(40) 5th: 0.0815
...
純正4度で`うなり'を 0.6とした場合です。
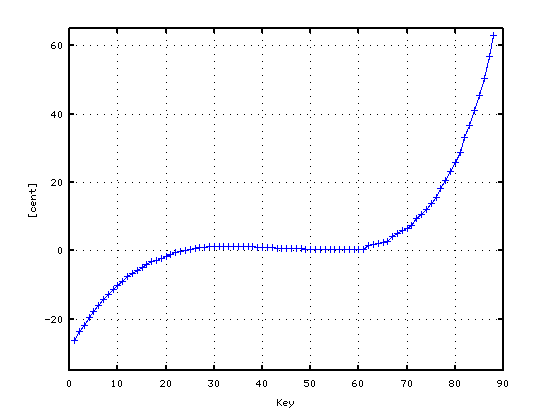
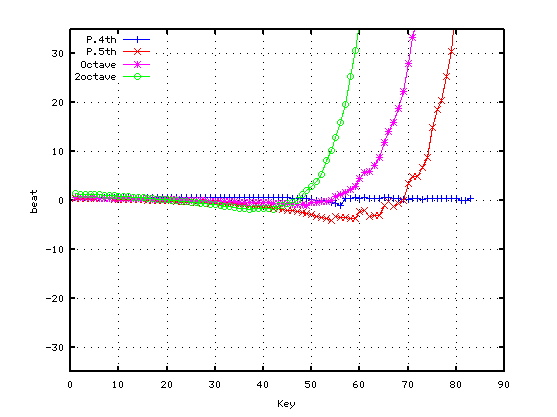
A(37)-D(42) 4th: 0.5561
G(35)-D(42) 5th: -0.9453
G(35)-C(40) 4th: 0.5626
F(33)-C(40) 5th: -0.7736
...
2オクターブで`うなり'を 1.0とした場合です。
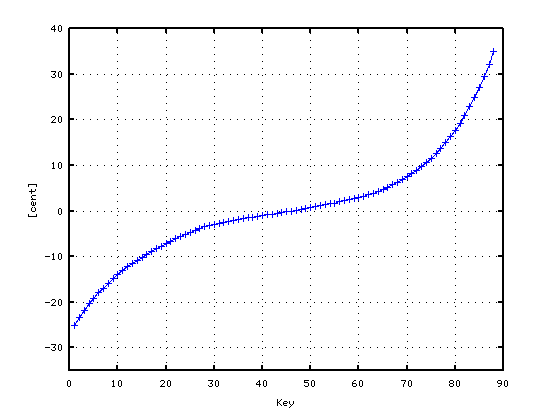
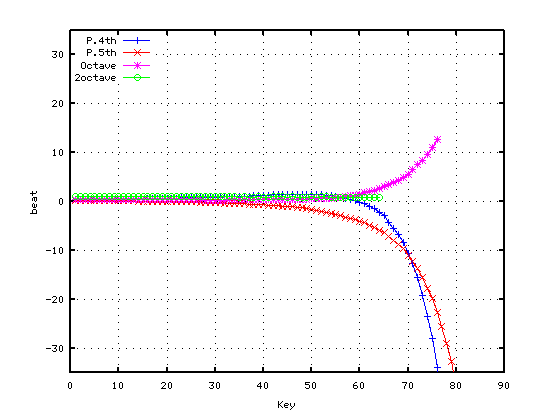
A(37)-D(42) 4th: 1.1492
G(35)-D(42) 5th: -0.4122
G(35)-C(40) 4th: 1.0603
F(33)-C(40) 5th: -0.3189
...
低音部の A(1)〜Gis(12)は 10:5の倍音で・
A(13)〜Gis(24)は 8:4で・A(25)〜G(35)は 6:3で・
B(62)〜C(88)は 2:1と分割して
`うなり'を 0.0で合わせた場合です。
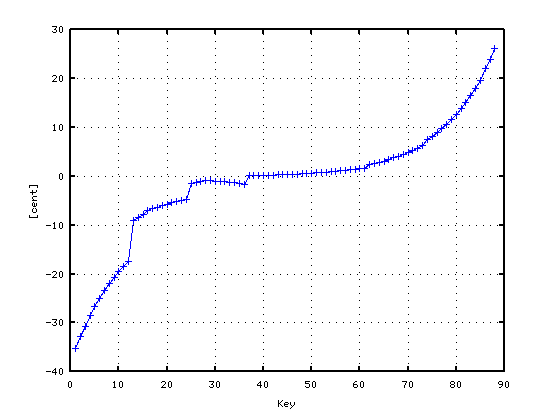
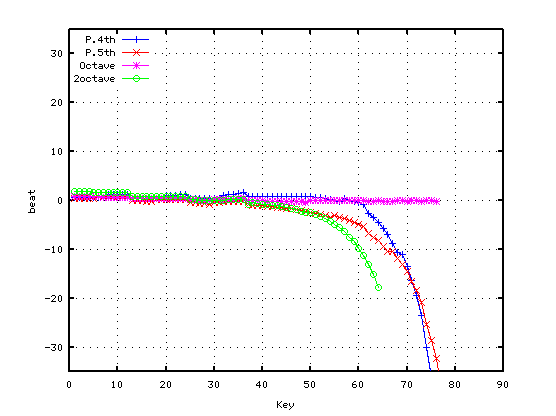
A(37)-D(42) 4th: 0.8105
G(35)-D(42) 5th: -0.1973
G(35)-C(40) 4th: 1.4690
F(33)-C(40) 5th: -0.2586
...
それぞれの場合で オクターブの`うなり'を
6倍音まで(2:1〜12:6)拡大して見てみます。
オクターブの場合です。
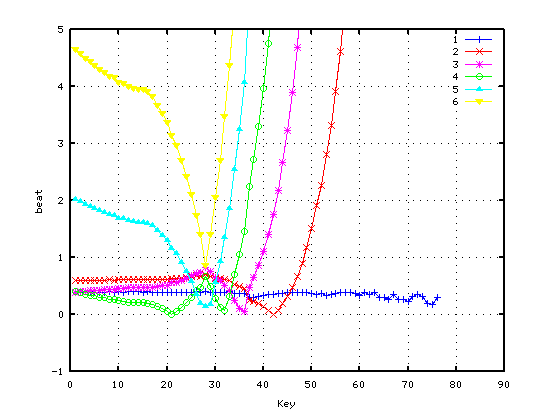
純正5度の場合です。
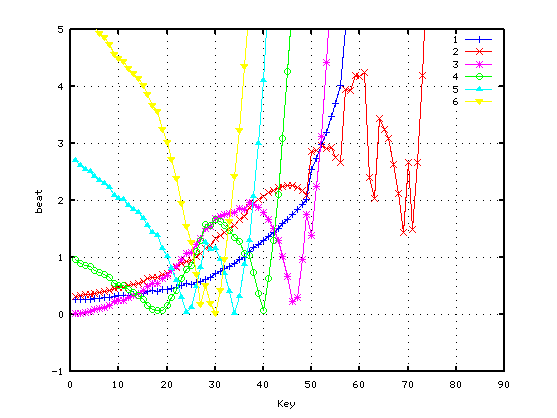
純正4度の場合です。
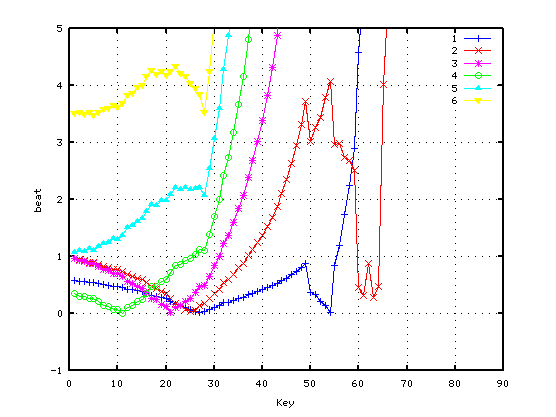
2オクターブの場合です。
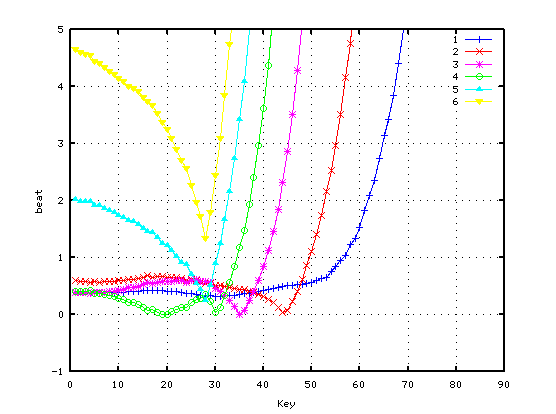
オクターブで分割した場合です。
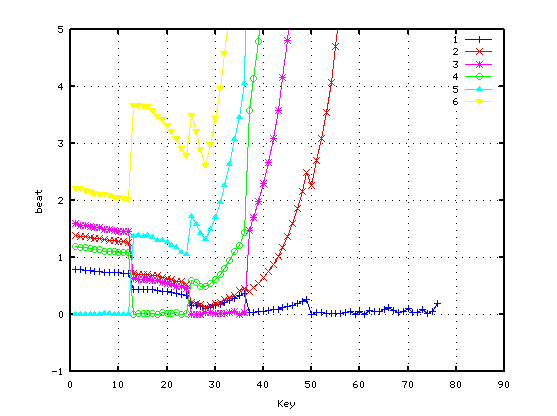
それぞれで C(4)のみのオクターブの`うなり'を
8倍音まで(2:1〜16:8)取り出して見てみます。
オクターブの場合です。
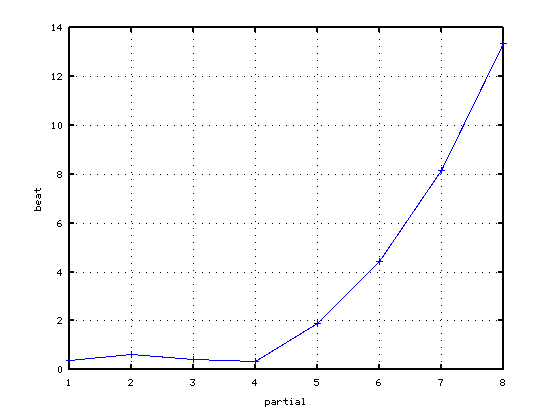
純正5度の場合です。
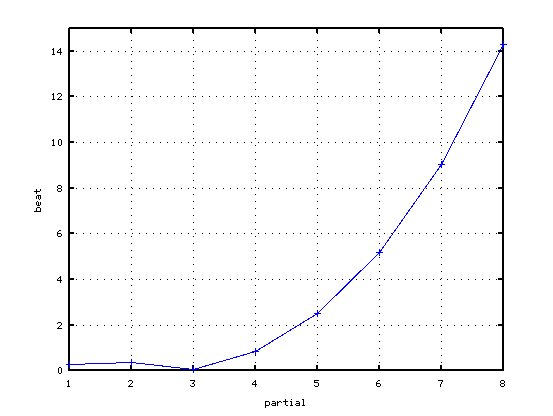
純正4度の場合です。
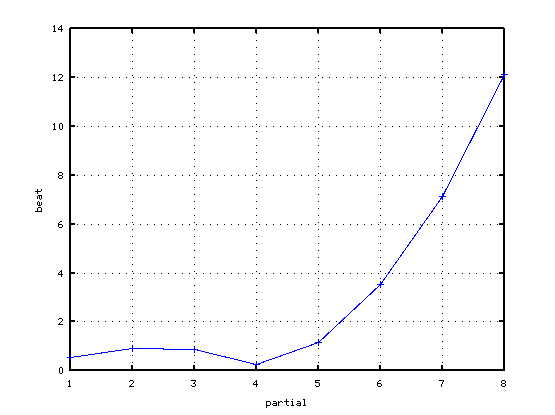
2オクターブの場合です。
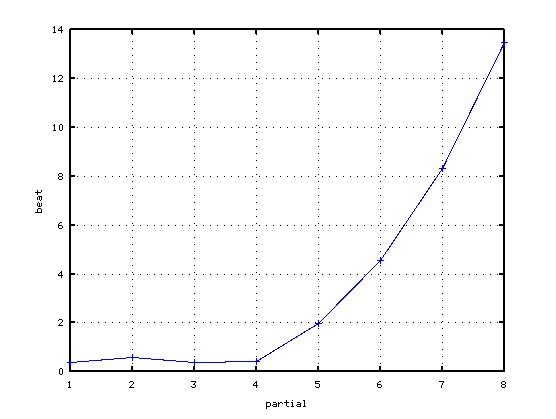
オクターブで分割した場合です。
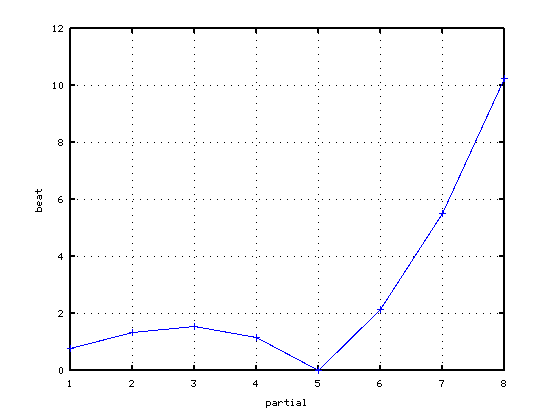
2オクターブの場合
経験的に行って来た`2オクターブでチェック'
割振りは`四度 三つ・五度 一つ'が対応する様ですし
サンダーソン式にも(サンダーソン式のセント値と`うなり'です。)
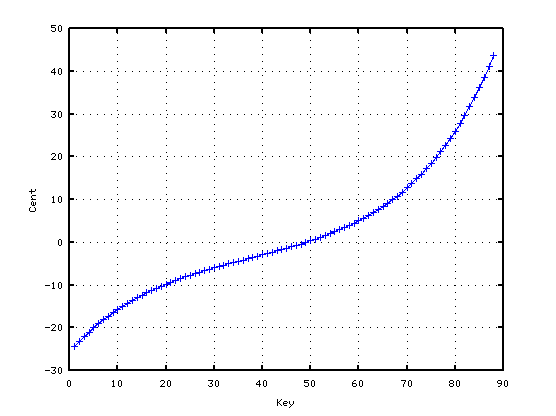
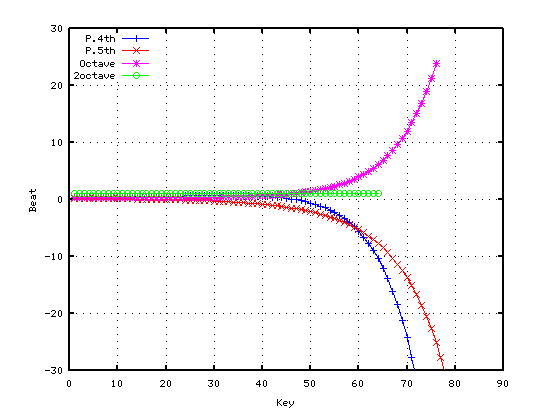
対応している様に思われます。
(※v0.1.1)以後には
「Non Zero方式」
巻線の調律シミュレーション
(Tuning Simulation of Wound Wire)
「エンベロープ方式」
エンベロープのシミュレーション(Simulation of Envelope)
などがあります。
参照>
変更履歴:
v0.1.2['16/09/25] 調律曲線(セント値)表示への注意を加えました。
v0.1.1['15/09/13] 以後のTuning方式への参照を追加しました。
v0.1['11/01/28]
Dobashi.M
Last modified: 1月 03日 火 15:15:52 2023 JST






















