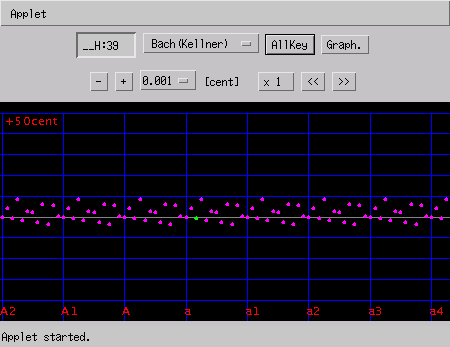
平均律 (Equal Temperament) の場合の割り振りの範囲の'うなり'です。
Key# : [Hz]: [Cent]: Mj-3rd: P-4th: P-5th: Octave ---------------------------------------------------- __F 33 174.6141 0.0000 6.9294 0.7892 -0.5912 0.0000 Fis 34 184.9972 0.0000 7.3415 0.8361 -0.6264 0.0000 __G 35 195.9977 0.0000 7.7780 0.8858 -0.6636 0.0000 Gis 36 207.6523 0.0000 8.2405 0.9385 -0.7031 0.0000 __A 37 220.0000 0.0000 8.7305 0.9943 -0.7449 0.0000 __B 38 233.0819 0.0000 9.2497 1.0534 -0.7892 0.0000 __H 39 246.9417 0.0000 9.7997 1.1161 -0.8361 0.0000 __C 40 261.6256 0.0000 10.3824 1.1824 -0.8858 0.0000 Cis 41 277.1826 0.0000 10.9998 1.2527 -0.9385 0.0000 __D 42 293.6648 0.0000 11.6539 1.3272 -0.9943 0.0000 _Es 43 311.1270 0.0000 12.3468 1.4062 -1.0534 0.0000 __E 44 329.6276 0.0000 13.0810 1.4898 -1.1161 0.0000 __F 45 349.2282 0.0000 13.8588 1.5784 -1.1824 0.0000
Key to Key :音程:うなり -------------------------- A -> D 4度 0.9943 G <- D 5度 -0.6636 G -> C 4度 0.8858 F <- C 5度 -0.5912 ...
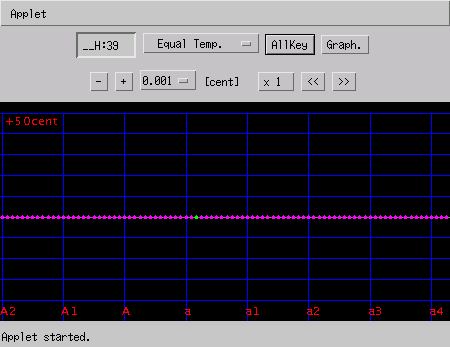
A(37) 220[Hz]で4度の'うなり'数が 数値の上では 0.9943で ほとんど 1だから「1秒にうなり1つ」と思ってしまいます。
しかし 先生(師匠)からは「4度3つ,5度1つ」と教わります。
…?
始めはいつまで経っても割り切れませんが
確かに4度1つではあまりに余ってしまいます。
では 調律曲線であればいいのでしょうか?
調律曲線 (Tuning Curve)のみ場合です。
Key# : [Hz]: [Cent]: Mj-3rd: P-4th: P-5th: Octave ---------------------------------------------------- __F 33 174.6141 0.0000 6.9294 0.7892 -0.2889 0.4037 Fis 34 184.9972 0.0000 7.3415 1.2641 -0.3061 0.4277 __G 35 195.9977 0.0000 8.3487 1.3393 -0.3243 0.4531 Gis 36 207.6523 0.0000 8.8452 1.4190 0.0162 0.7203 __A 37 220.0000 0.0000 9.3711 1.5033 0.0172 0.7631 __B 38 233.0819 0.0000 9.9284 2.1323 0.0182 0.8085 __H 39 247.0843 1.0000 10.5248 1.6884 -0.4088 0.5712 __C 40 261.7767 1.0000 11.1507 1.7888 -0.4331 0.9080 Cis 41 277.3428 1.0000 11.8137 1.8952 0.0216 0.9620 __D 42 293.8344 1.0000 12.5162 2.0079 0.0229 1.0192 _Es 43 311.4866 2.0000 12.3611 2.1285 -0.5153 0.7201 __E 44 330.0086 2.0000 14.0571 2.2551 -0.5460 0.7629 __F 45 349.6319 2.0000 14.8929 2.3892 0.0273 1.2128
Key to Key :音程:うなり -------------------------- A -> D 4度 1.5033 G <- D 5度 -0.3243 G -> C 4度 1.3393 F <- C 5度 -0.2889 ...
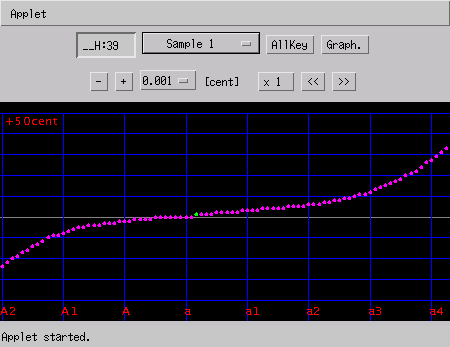
確かに4度は増えましたが 5度が不確かではあります。
…?
そして,やがて「インハーモニシティ」なるものがある事を知ります。
インハーモニシティ(Inharmonicity)のみの場合です。
No.: Key: Name: [Hz]: [cent]: Mj-3rd: P-4th: P-5th: Octave ---------------------------------------------------------- _52: _33: __F: 174.614: 0.0: 6.223: 0.383: -0.787: -0.067 _53: _34: Fis: 184.997: 0.0: 6.826: 0.546: -0.782: -0.062 _54: _35: __G: 195.997: 0.0: 7.384: 0.595: -0.807: -0.062 _55: _36: Gis: 207.652: 0.0: 7.936: 0.734: -0.815: -0.055 _56: _37: __A: 220.0__: 0.0: 8.423: 0.777: -0.87 : -0.059 _57: _38: __B: 233.081: 0.0: 8.943: 0.823: -0.921: -0.074 _58: _39: __H: 246.941: 0.0: 9.375: 0.806: -1.039: -0.09 _59: _40: __C: 261.625: 0.0: 10.061: 0.935: -1.091: -0.086 _60: _41: Cis: 277.182: 0.0: 10.641: 0.834: -1.174: -0.118 _61: _42: __D: 293.664: 0.0: 10.936: 0.799: -1.25 : -0.097 _62: _43: _Es: 311.126: 0.0: 11.435: 0.817: -1.414: -0.13 _63: _44: __E: 329.627: 0.0: 12.111: 0.896: -1.523: -0.155 _64: _45: __F: 349.228: 0.0: 12.836: 0.634: -1.626: -0.18
Key to Key :音程:うなり ------------------------- A -> D 4度 0.777 G <- D 5度 -0.807 G -> C 4度 0.595 F <- C 5度 -0.787 ...
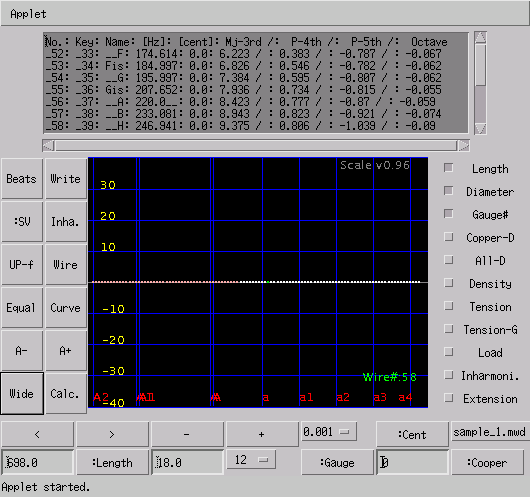
それに サンプルの調律曲線を出して見ます。
インハーモニシティ + 調律曲線 (Inharmonicity + Tuning Curve)の場合です。
No.: Key: Name: [Hz]: [cent]: Mj-3rd: P-4th: P-5th: Octave ---------------------------------------------------------- _52: _33: __F: 174.614: 0.0: 6.223: 0.383: -0.485: 0.336 _53: _34: Fis: 184.997: 0.0: 6.826: 0.973: -0.462: 0.366 _54: _35: __G: 195.997: 0.0: 7.953: 1.048: -0.468: 0.391 _55: _36: Gis: 207.652: 0.0: 8.54 : 1.213: -0.097: 0.665 _56: _37: __A: 220.0__: 0.0: 9.062: 1.286: -0.109: 0.704 _57: _38: __B: 233.081: 0.0: 9.619: 1.9 : -0.114: 0.734 _58: _39: __H: 247.084: 1.0: 10.098: 1.378: -0.612: 0.482 _59: _40: __C: 261.776: 1.0: 10.827: 1.54 : -0.638: 0.821 _60: _41: Cis: 277.342: 1.0: 11.452: 1.475: -0.215: 0.843 _61: _42: __D: 293.834: 1.0: 11.796: 1.478: -0.233: 0.922 _62: _43: _Es: 311.486: 2.0: 11.45 : 1.538: -0.876: 0.589 _63: _44: __E: 330.008: 2.0: 13.084: 1.66 : -0.954: 0.607 _64: _45: __F: 349.631: 2.0: 13.866: 1.443: -0.418: 1.032
Key to Key :音程:うなり ------------------------- A -> D 4度 1.286 G <- D 5度 -0.468 G -> C 4度 1.048 F <- C 5度 -0.485 F -> B 4度 0.383 B -> Es 4度 1.9 B -> F 5度 -0.114 (C <- F 4度 1.54) Gis <- Es 5度 -0.097 Gis -> Cis 4度 1.213 Fis <- Cis 5度 -0.462 Fis -> H 4度 0.973 H -> E 4度 1.378 (A <- E 5度 -0.109)
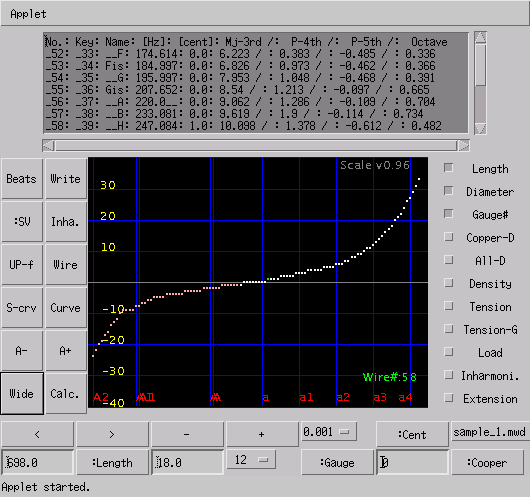
初めの 4度(A) 5度(G)の'うなり'の比が 約3対1と現されました。
この事だったのですね。
その後 Java Tuner で様々なピアノ弦を試してみた所 以下の様な例もあります。
sample_1 を 2.0[cent]で [Laying]を行った場合です。
Wire#:Key# [Hz]: : [cent] : Octave 2:1 : P4th P5th ------------------------------------------------------ 52:33<F..>174.565: -0.483: 0.067: 0.719: -0.435 53:34<Fis>184.963: -0.323: 0.045: 0.902: -0.408 54:35<G..>195.981: -0.151: 0.014: 0.972: -0.411 55:36<Gis>207.654: 0.017: -0.015: 1.133: -0.396 56:37<A..>220.025: 0.199: -0.059: 1.201: -0.426 57:38<B..>233.133: 0.382: -0.119: 1.271 58:39<H..>247.023: 0.573: -0.185: 1.282 59:40<C..>261.739: 0.752: -0.237 60:41<Cis>277.334: 0.944: -0.332 61:42<D..>293.858: 1.138: -0.38 62:43<Es.>311.367: 1.334: -0.49 63:44<E..>329.919: 1.531: -0.599
Key to Key :音程:うなり ------------------------- A -> D 4度 1.201 G <- D 5度 -0.411 G -> C 4度 0.972 F <- C 5度 -0.435 ...
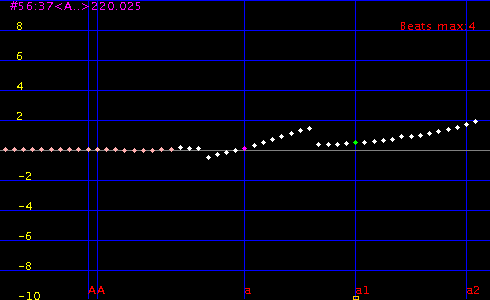
sample_1 を Inter. 1.0[beats] で [2Octave]を行った場合です。
Wire#:Key# [Hz]: : [cent] : Octave 2:1 : P4th : P5th ----------------------------------------------------- 52:33<F..>174.313: -2.992: 0.462: 1.053: -0.2 53:34<Fis>184.731: -2.492: 0.421: 1.099: -0.278 54:35<G..>195.758: -2.121: 0.397: 1.077: -0.351 55:36<Gis>207.445: -1.733: 0.371: 1.125: -0.422 56:37<A..>219.807: -1.516: 0.377: 1.16: -0.478 57:38<B..>232.908: -1.292: 0.369: 1.19 58:39<H..>246.78: -1.131: 0.379: 1.196 59:40<C..>261.477: -0.981: 0.411 60:41<Cis>277.052: -0.818: 0.408 61:42<D..>293.554: -0.654: 0.46 62:43<Es.>311.039: -0.488: 0.46 63:44<E..>329.567: -0.32: 0.471
Key to Key :音程:うなり ------------------------- A -> D 4度 1.16 G <- D 5度 -0.351 G -> C 4度 1.077 F <- C 5度 -0.2 ...
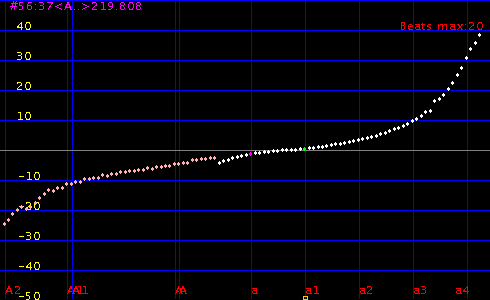
ピアノ弦のインハーモニシティ値の差異(ピアノの差異)・ 割り振りの採り方により多少の差異があります。
(※)参考までに サンダーソン式の場合を追加します。
Key#() : [Hz]:[cent]:P-4th: P-5th: Octave -------------------------------------------- 33 (F) : 174.11: -5.01: 0.70: -0.38: 0.49 34 (Fis): 184.49: -4.71: 0.70: -0.43: 0.51 35 (G) : 195.50: -4.41: 0.69: -0.48: 0.53 36 (Gis): 207.16: -4.11: 0.67: -0.54: 0.56 37 (A) : 219.52: -3.81: 0.66: -0.61: 0.59 38 (B) : 232.61: -3.52: 0.63: -0.67: 0.62 39 (H) : 246.48: -3.22: 0.60: -0.75: 0.65 40 (C) : 261.18: -2.92: 0.57: -0.83: 0.69 41 (Cis): 276.76: -2.62: 0.52: -0.91: 0.74 42 (D) : 293.27: -2.32: 0.46: -1.01: 0.79 43 (Es) : 310.77: -2.01: 0.40: -1.11: 0.84 44 (E) : 329.31: -1.69: 0.32: -1.22: 0.91 45 (F) : 348.95: -1.37: 0.22: -1.34: 0.98
Key to Key :音程:うなり ------------------------ A -> D 4度 0.66 G <- D 5度 -0.48 G -> C 4度 0.69 F <- C 5度 -0.38 ...
例えば「スミソン氏の遺骨」(Mr.SMITHSON'S BONES) リチャード・T・コンロイ 1993年(創元推理文庫)に チェンバロを調律する下りがあります。
『…音叉を使って正確なA音に合わせた。
…毎秒一回のうなりが出るように四度音程をひろげ, …これで…再調律しなくても,自由に転調できる。』
(Aは440[Hz]。下線は筆者)
しかし それでは 1.の平均律そのままです。
その場合は古典調律,例えばバッハの「Wholtemperierung」
(気持ち良い調律)などが適っている様に思われます。
バッハ(ケルナー) (Bach - Well Tempered By Kellner)の場合です。
Key# : [Hz]: [Cent]: Mj-3rd: P-4th: P-5th: Octave ------------------------------------------------------- __F 33 175.2406 6.2000 3.7971 0.0223 0.0137 0.0000 Fis 34 184.6236 -3.5000 11.5282 2.0311 -0.0176 0.0000 __G 35 196.6214 5.5000 4.2604 2.1176 -1.5839 0.0000 Gis 36 207.7003 0.4000 12.9691 -0.0216 -0.0198 0.0000 __A 37 220.0000 0.0000 7.7063 2.4203 -1.7722 0.0000 __B 38 233.6615 4.3000 8.2528 -0.0243 -0.0223 0.0000 __H 39 246.8418 -0.7000 11.9533 -0.0257 -2.0311 0.0000 __C 40 262.8677 8.2000 2.1170 -0.0273 -2.1176 0.0000 Cis 41 276.9266 -1.6000 17.2917 0.0352 0.0216 0.0000 __D 42 294.1401 2.8000 6.2881 3.1678 -2.4203 0.0000 _Es 43 311.5406 2.3000 15.2680 0.0396 0.0243 0.0000 __E 44 329.1139 -2.7000 16.0333 3.5445 0.0257 0.0000 __F 45 350.4811 6.2000 7.5942 0.0445 0.0273 0.0000
Key to Key :音程:うなり -------------------------- A -> D 4度 -0.0216 G <- D 5度 -1.5839 G -> C 4度 2.1176 F <- C 5度 0.0137 ...