(変更履歴:
v0.4['19/06/09]
Tuningのシミュレーションを[Tune3]に変更しました。
[Beat]表示を元の単数の音程のみとして
倍音数での表示に戻しました。
v0.3['16/09/11]
[Cent]表示にインハーモニシティ値を加えなくしました。
[Beat]表示を複数の音程可能にしました。
v0.2['15/08/02]
エンベロープ部分を共通用としてEnvelope.jsに分離しました。
TuneEの高音部もエンベロープに対応しました。
v0.1.4['15/02/21]
[D(amping)]ボタンを止めて スライダーに変更しました。
[Beat] ビート表示を追加しました。
平均律での例を追記しました。
v0.1.2['14/12/23]
[D(amping)]Wave信号の減衰ボタンを追加しました。
v0.1['14/09/15])
上側セレクタ[Inha(rmonicity)]: インハーモニシティ値を表示します。
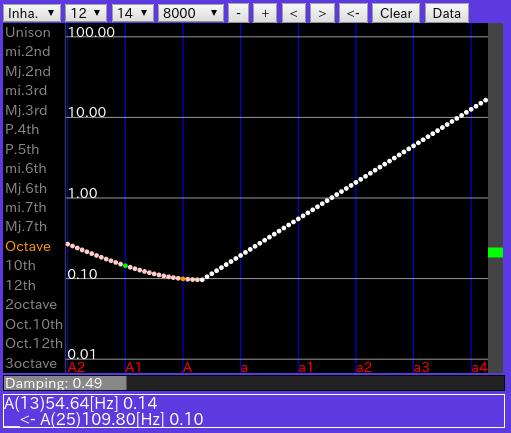
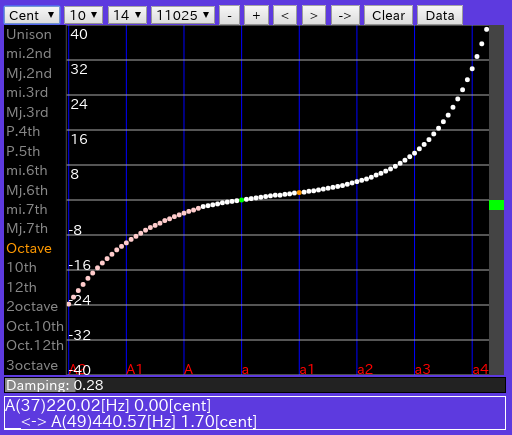
[Cent]: セント値を表示します。 (v0.3)インハーモニシティ値を加えなくしました
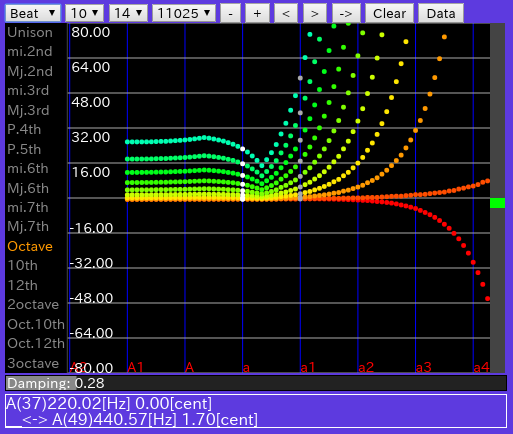
[Beat]: キー全体の'うなり'を表示します。
(v0.3)複数の音程を表示するように変更しました。
(※v0.4)以前の倍音数での表示に戻しました。
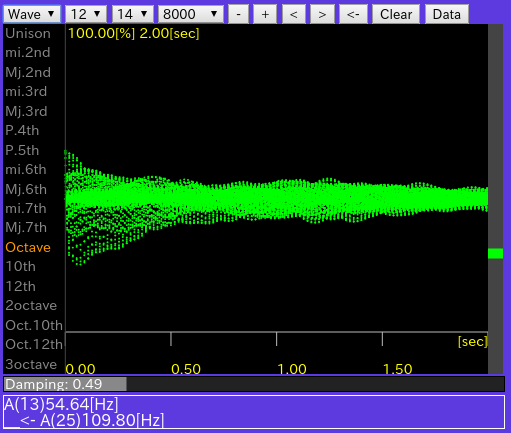
[Wave]: Wave信号を表示します。
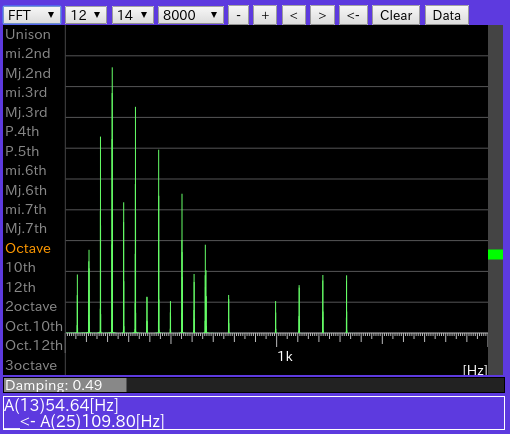
[FFT]: Wave信号の FFTスペクトルを表示します。
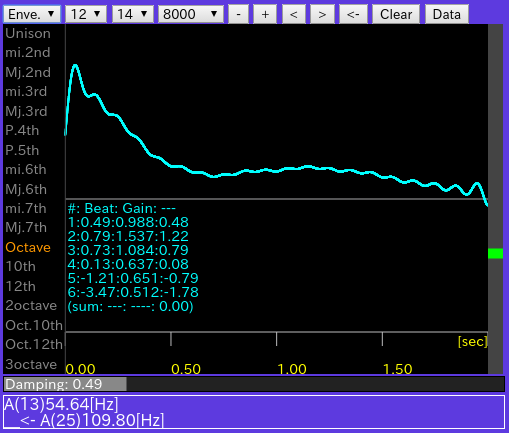
[Enve(lope)]: Wave信号の包絡線(Envelope)を表示します。
[ 1 ... 20 ]: 倍音数を選択します。 「エンベロープで見る'うなり'(Beat and Envelope)」との違いは [FFT]で見ると分かるように 音程が重なる倍音が対象となります。
[ 9 ... 14 ]: [FFT]のサンプル数(2^X)を選択します。
(9:512 10:1024 11:2048 12:4096 13:8192 14:16384)
[ 8000 ... 44100 ]: Wave信号のサンプリング周波数を選択します。
[ - ][ + ]: [Inha]以外のグラフの高さを増減します。
[ < ][ > ]: [FFT]でグラフの幅を増減します。
[ <- | -> ]: 音程を採る方向を示します。 カーソルキーを緑色で 対象キーは音程のカラーで表しています。
(※v0.4)[ Tune3 | Clear]:
Tuning3のシミュレーションを行います。
ただし低音側のみで
Envelopeが少なくなる様な値に設定しています。
(v0.2)高音側もEnvelopeが少なくなる様な値に設定しました。
(その時にとる低音部の倍音の範囲は
倍音数のセレクタで選択出来ます。)
[ Data ]: [Enve.]でデータの表示をOn-Offします。
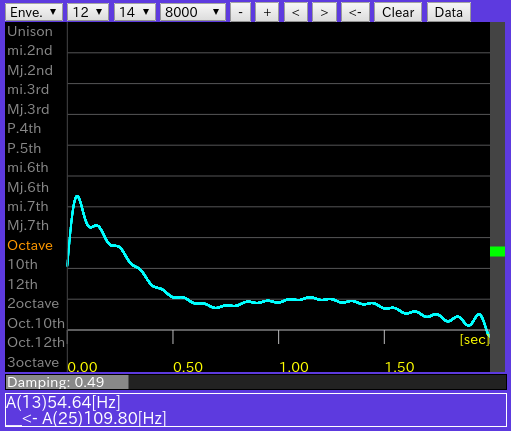
下側[ Damping: 1.0 ] スライダー: カーソルのドラッグでWave信号の減衰量を増減します。
左側[ Unison ... 3octave ]: 音程を選択します。 (v0.3)複数の音程を選択出来るようになりました。 その時 最後に選んだ音程が[Wave][FFT]などに使用されます。
右側: カーソルキーのセント値を表示して ドラッグでセント値を増減します。
画面下:
[ A(13)55.00[Hz] 0.14 ]
[__<- A(25)110.01[Hz] 0.10 ]
[ カーソルのキー名 周波数[Hz] *値 ]
[__<- 音程のキー名 周波数[Hz] *値 ]を表示します。
[*値]は[Inha.]時は"インハーモニシティ値"を それ以外では"セント値[cent]"を表示します。
![equal cent 0[cent]](./gifsm/equal-cent-0.png)
![equal beat 0[cent]](./gifsm/equal-beat-0.png)
![equal fft 0[cent]](./gifsm/equal-fft-0.png)
![equal enve. 0[cent]](./gifsm/equal-enve-0.png)
![equal wave 0[cent]](./gifsm/equal-wave-0.png)
![equal cent 8[cent]](./gifsm/equal-cent-p8.png)
![equal beat 8[cent]](./gifsm/equal-beat-p8.png)
![equal fft 8[cent]](./gifsm/equal-fft-p8.png)
![equal enve. 8[cent]](./gifsm/equal-enve-p8.png)
![equal wave 8[cent]](./gifsm/equal-wave-p8.png)
![equal cent -8[cent]](./gifsm/equal-cent-m8.png)
![equal beat -8[cent]](./gifsm/equal-beat-m8.png)
![equal fft -8[cent]](./gifsm/equal-fft-m8.png)
![equal enve. -8[cent]](./gifsm/equal-enve-m8.png)
![equal wave -8[cent]](./gifsm/equal-wave-m8.png)
![equal cent -16[cent]](./gifsm/equal-m16-cent.png)
![equal beat -16[cent]](./gifsm/equal-m16-beat.png)
![equal fft -16[cent]](./gifsm/equal-m16-fft.png)
![equal enve. -16[cent]](./gifsm/equal-m16-enve.png)
![equal wave -16[cent]](./gifsm/equal-m16-wave.png)