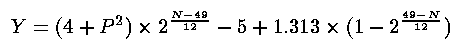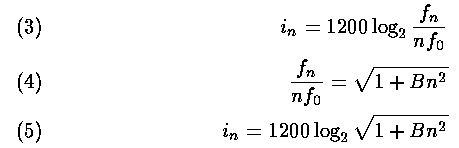インハーモニシティについて (Inharmonicity) v0.8
(※)インハーモニシティとは?
(※3)『インハーモニシティは、弦の曲げに対する抵抗力に起因しており、
弦の材質が硬いほど、また、
弦の直径が大きいほどインハーモニシティは大きくなります。
長さについては、短い弦ほどインハーモニシティが大きくなります。』
(※1)『...ハーモニックな部分音は無限に細い直径によってのみ現れる。
けれども、実際には不可能である。
太い弦の場合、弦の硬直性はそれだけで高まる。
それによって部分音の振動数も高まる。
これは整数比の中には現れず、それゆえインハーモニックになる。』
(※4)『弦の振動数と、これによって出る音を初等力学で扱う場合は、
普通、部分音が整数倍のいわゆる倍音構造として解析される。
しかしこれは、弦の太さ、あるいは剛性を無視できる、
いわば物理的に理想的な弦である場合で、
実際はこういう弦は存在しないから、正確には、整数倍からずれてくる。
ヴァイオリンやチェロなどの弦ではこの非整数倍性は無視できるが、
ピアノではピアノ線という剛性の高い弦を用いているため
非整数倍性は大きく、
これがピアノ音らしい音色の重要な要因になっている。』
(非整数倍性 ≒ インハーモニシティ)
《参照》
「ピアノ弦の倍音理論」
"Harmonic Overtone Theory of Piano Strings"
アルバート・サンダーソン氏 (Albert Sanderson)のセミナーより
以下の公式を得ました。
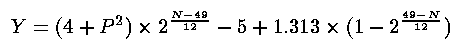
[Y=セント値(Cent):P=倍音(Partial#):N=キー番号(Key#)]
《アメリカ特許 5285711》
その式は「ピアノの調律曲線」を表します。
それをグラフにして見ました。
(図をクリックして下さい。拡大されます。)
P = 1の場合です。
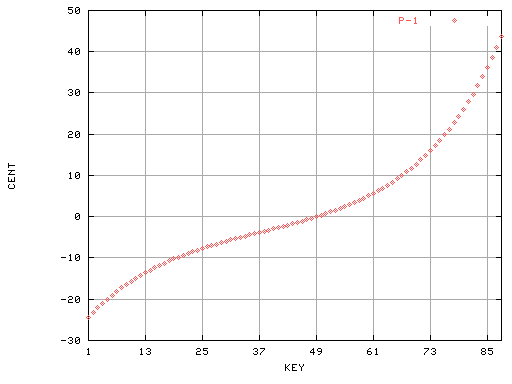
P = 1〜8までを重ねて見ます。
text
(※v0.8)[Beat]ボタンを押して下さい。
倍音のセント値から周波数値を求めて 音程間の周波数差
'うなり'を求めてみます。
(※v0.8)[Text]ボタンを押して下さい。
ドラッグしたキーを中心に 1オクターブの周波数を取り出して見ます。
[Beat]の場合は'うなり'の値を表示します。
A49(440[Hz])の 2倍音は
1オクターブ上の A61から(882.88-881.53=)1.35となります。
3倍音は E56の 2倍音(5度)から(1324.18-1326.11=)-1.94となります。
4倍音は D54の 3倍音(4度)から(1774.94-1775.32=)-0.37となります。
(※v0.8)下2桁で四捨五入して表示しましたので
計算値に多少の誤差があります。
「続 サンダーソン式
(Sanderson)」
「
サンダーソン氏の計算式を分解すると...?」
ちなみに平均律の場合の'うなり'です。
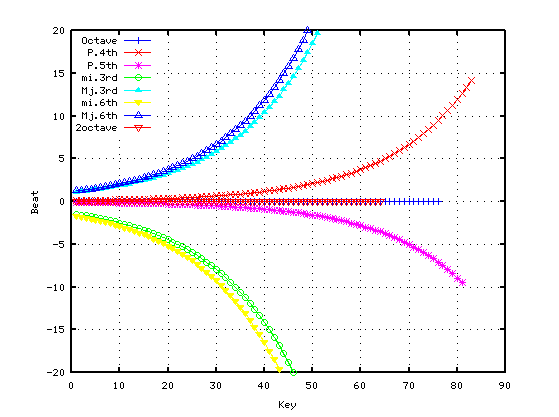
オクターブ・2オクターブ...は皆 0になります。
実際にピアノを設計する時には中央
A49のインハーモニシティ値を決めてから
88鍵の弦をスケーリングして行きます。
A49のインハーモニシティが 0.6より大きい時は音色は鋭くなり
0.5よりも小さい時は柔らかい音色になるようです。
ピアノ弦の性質として以下の式があります。
δ = K x d2 / (l4 x f2)
《※1:ヤングの公式》
- δ = インハーモニシティ値
- d = 弦径
- l = 弦長
- f = 振動数
- K = 係数(経験値として 3.3 x 1015)
インハーモニシティ値とキーの周波数から
全体の張力が一定になる様に弦径(番手)と弦長を決めて行きます。
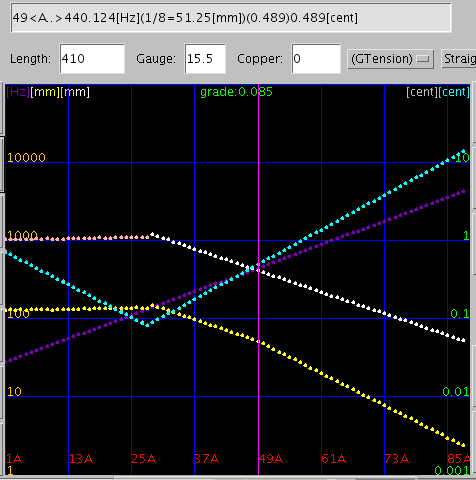
シアン色でインハーモニシティ値を
白色で弦長(ピンク色は巻線)
を表しています。
それを実際の弦長で表すと以下のようになります。
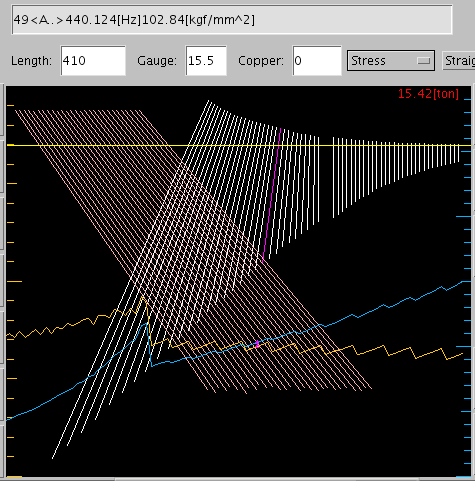
最近ではフレッチャーの式(※2)が使われています。


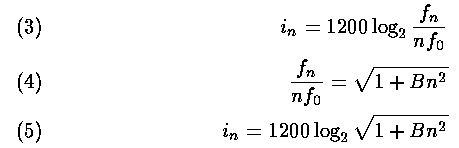
- in : インハーモニシティ値 [cent]
- f0 : 基音周波数 [Hz]
- n : 次数(倍音)Partial
- d : 線径 Diameter
- l : 弦長 Length
- T : 張力 Tension
- B : 定数 Constant
- E : 縦弾性係数(ヤング率)
ピアノでは硬鋼線(2.15x100000[N/mm2])を
フォルテピアノでは洋白線(1.08x100000[N/mm2])を使用します。
- 「Java Tuner」
また インハーモニシティの高次倍音には
以下の計算式が適用されます。
T = P x P x I
例えばあるキーでのインハーモニシティ値が 0.5[cent]とすると
第2倍音のインハーモニシティ値は 2 x 2 x 0.5 = 2.0[cent]となり
第3倍音では 3 x 3 x 0.5 = 4.5[cent]となります。
オクターブで例に取ると
A49を 0.55[cent]とすると A49の基音は 1x1x0.55...440.14[Hz]で
2倍音は 2x2x0.55 = 2.20...881.12[Hz]となるのに
合わせようとする A61は 1.528[cent] そのまま(平均律の周波数)では
1x1x1.528...880.777[Hz]ですので より高くなる方に動かします。
そうして調律曲線のレイルスバック・ストレッチが現れます。
「
傾き(grade)は2種類ある?」
「
インハーモニシテの計算について
(Rhapsody Inharmonicity)」
では低音では逆にインハーモニシティ値が大きくなるのだから
周波数は高くなるのでは? と思うかも知れません。
しかし「
低音では 10倍音で合わせる?」で見るように
倍音の'うなり'を少くする為により低く合わせるようになります。
(※v0.8)設計例として
以下の様なインハーモニシティ値を設定してみます。
A49のインハーモニシティ値 0.55・巻線の数 28・
インハーモニシティ値の傾き(Grade) 0.087とします。
(※v0.8)[Cent][Tune3]のボタンを押して下さい。
Tuningのシミュレーションを行うと
上の様な調律曲線になります。
「
Java 調律シミュレーター (Java Tuning Simulator)」
(※v0.8)[Beat]ボタンを押して下さい。
様々な音程の'うなり'を見てみます。
(v0.7)参考までに「Steinway Model B Grand」「Erard Grand」
「Baldwin 9' Concert Grand」3台の 測定されたスケールを見てみます。
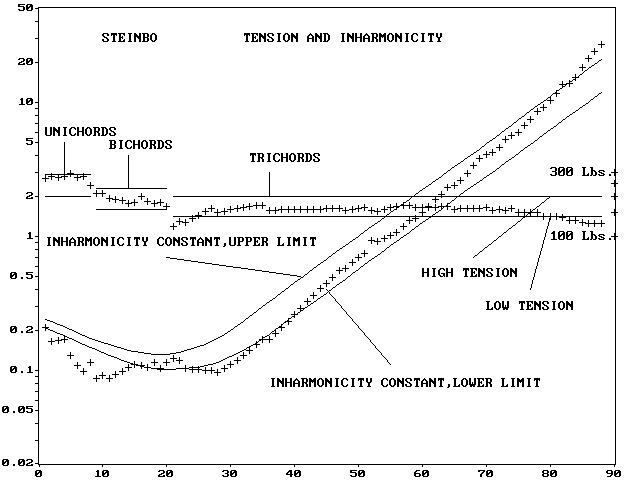
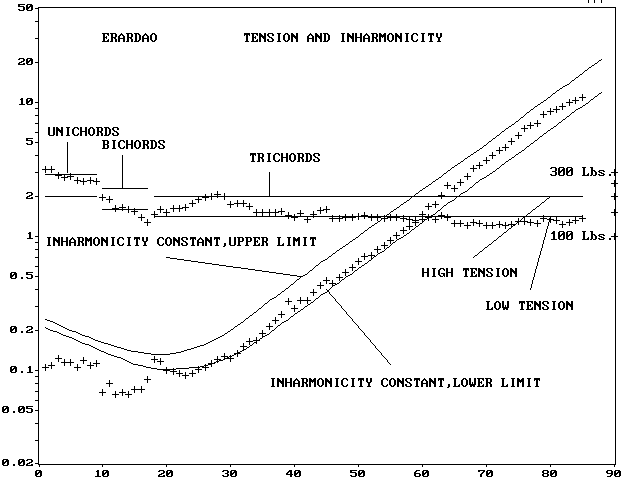
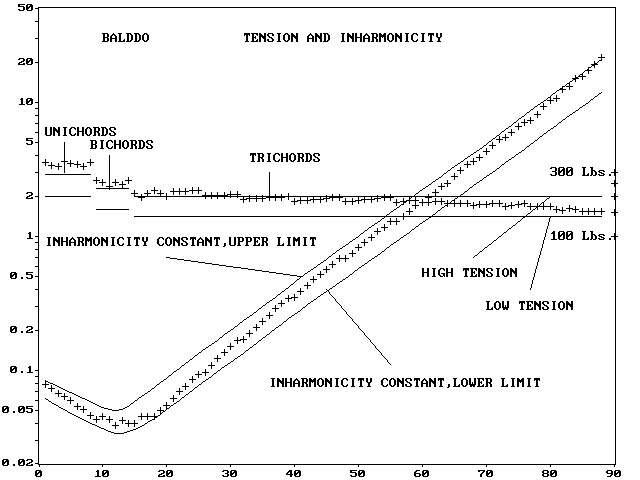
インハーモニシティ値と張力が示されています。
「
Computer Tools For Piano Technicians/The Scale Collection」
から引用させて頂きました。
(v0.5.3)因みにサンダーソン式から
インハーモニシティ値のみを取り出す事は出来るでしょうか?
- ih = インハーモニシティ値
- p2 = 2倍音のセント値
- p3 = 3倍音 "
- c0 = 元のセント値 (0でも可)
として 上方の式 T = P x P x I から
各倍音のセント値は
インハーモニシティ値と元になるセント値との合計で表されますので
p2 = 2 x 2 x ih + c0
p3 = 3 x 3 x ih + c0
それを入れ換えて
c0 = p2 - 4 x ih
c0 = p3 - 9 x ih
c0は同じなので無くすと
p3 - 9 x ih = p2 - 4 x ih
ihをまとめて
p3 - p2 = 9 x ih - 4 x ih
ihを一つにして
(9 - 4) x ih = p3 - p2
5 x ih = p3 - p2
と言う事で
ih = (p3 - p2) / 5
ihが得られました。
それを全てのキーで求めると 以下のグラフになります。
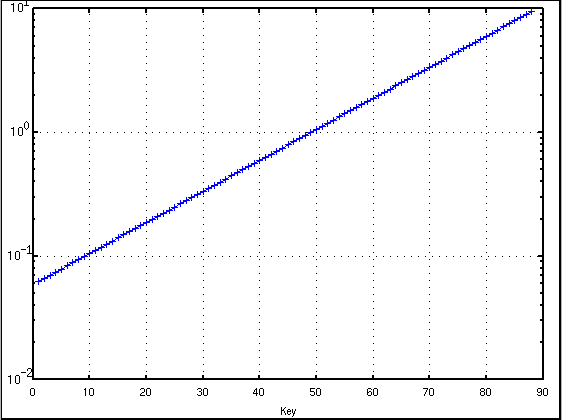
A49のインハーモニシティ値は 1.0,
C88のインハーモニシティ値は 9.5137,
から最小自乗法で求めた傾き(grade)は 0.0578となります。
サンダーソン式のP=1~8倍音までの図で
低音部の値が少ないのはインハーモニシティ値が
低音までずっと下がり続けているからと思われます。
《参照》
変更履歴:
v0.8['20/06/20] サンダーソン式とインハーモニシティ式を
Javascriptに変更しました。それに合わせて HTML5版としました。
v0.7['20/05/02]
インハーモニシティ値の測定例の表示と参照先を追加しました。
v0.6['16/09/23]
インハーモニシティ値の設計例を改めました。
v0.5.3['13/03/03]
サンダーソン式のインハーモニシティ値を追加しました。
v0.5.2['12/07/04] 引用文を追加しました。
v0.5.1['12/05/02] JavaScriptを分離しました。
v0.5['11/11/10] 周波数とc2fの計算式を修正しました。
v0.4['11/01/22] 低音について追記しました。
v0.3['10/12/30] 'うなり'の表示を
サンダーソン式・平均律・シミュレーション値の 3種類にしました。
v0.2['10/12/25] 少し省略しました。
参考文献
- (※1) Fachkunde Klavierbau -ピアノの構造とその関連技術- V.Laible著
畠 俊夫訳 東洋音楽専修学校 1991年
- (※2) 弦の非調和性がピアノの調律に与える影響 森 太郎
日本音響学会音楽音響研究会資料 MA00-37 2000年
- (※3) もっと知りたいピアノのしくみ 西口 磯春・森 太郎 共著
音楽之友社 2005年
- (※4) 楽器の音響学 安藤 由典 音楽之友社 1996年
Dobashi.M
Last modified: 1月 03日 火 09:22:04 2023 JST